Draw lines perpendicular to X axis and Y axis to a curve in matplotlib plot-CodePudding

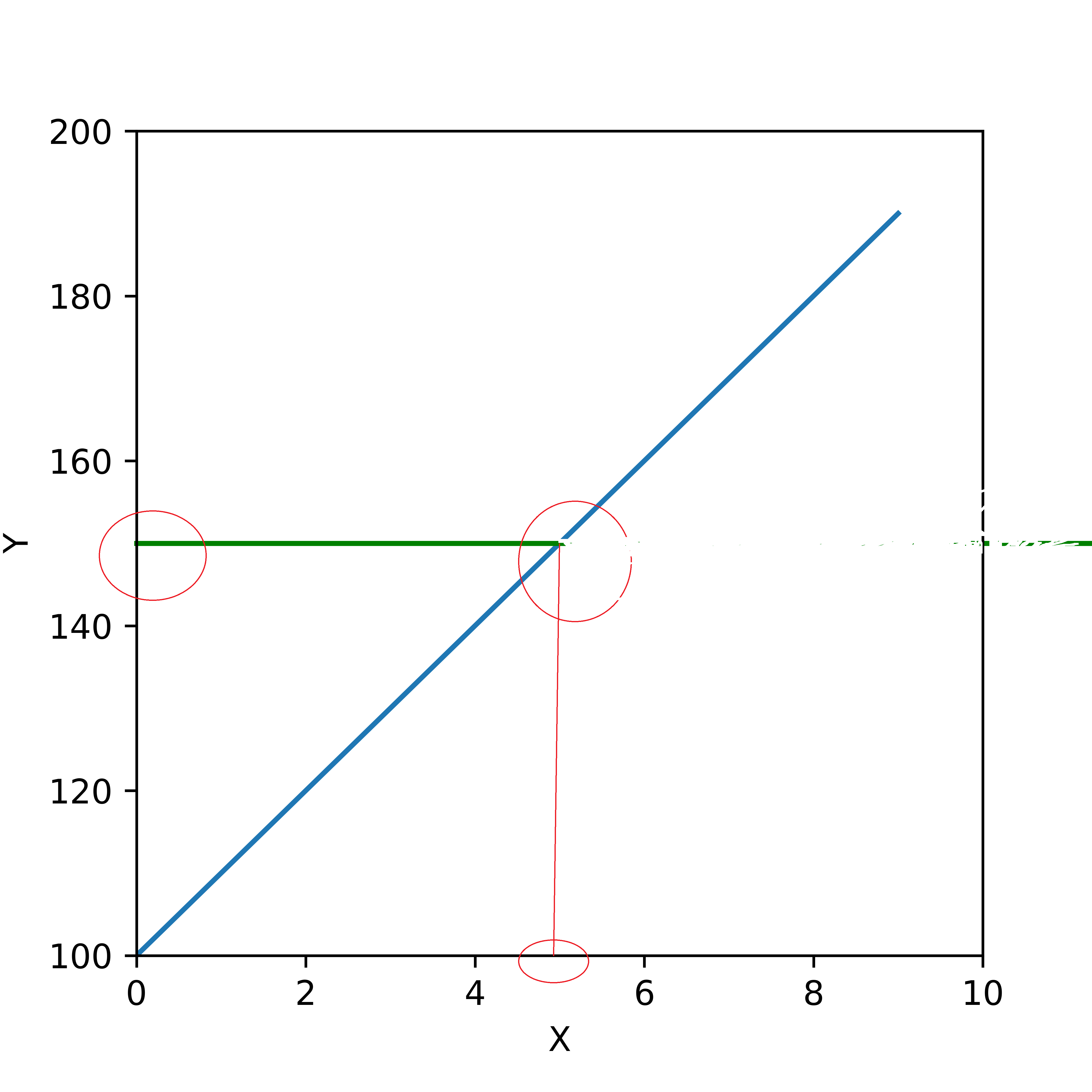
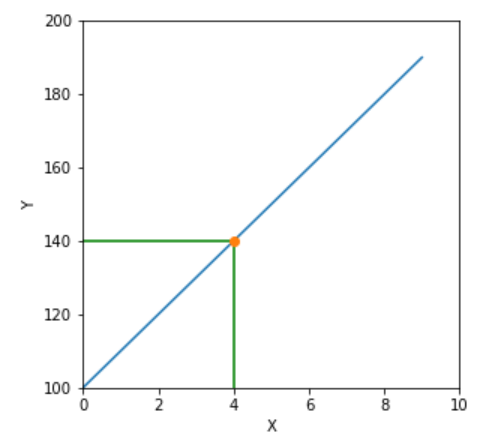
I am trying to plot a horizontal line from a selected point in Y-axis (say, y = 150, in our following sample data) to a curve (blue colored straight line in our sample plot). Then, from the point of intersection of horizontal line with the curve, I want to drop a line perpendicular to the X - axis. I tried following code line but I could not limit the value of parameter xmax such that the horizontal line ends exactly at the point of intersection with the curve. I also know that maximum limit of xmax = 1.0. For this case, xmax = 0.5 may give me the point of intersection. However, I want to implement this on more complex curves. Can somebody please advise me?

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


df = pd.DataFrame({'x': np.arange(10),
                   'y': np.arange(100, 200, 10)})

fig,ax = plt.subplots(figsize =(4.5,4.5))
ax.plot(df.x,df.y)

plt.xlabel('X')
plt.ylabel('Y')
plt.xlim(0,10)
plt.ylim(100,200)

# ax.axhline(y=150, xmin=-0.02, xmax=0.5, clip_on= True)
ax.axhline(y=150, xmin=0, xmax= df.loc[df['y'] == 150, 'x'].iloc[0], clip_on= False, color = 'Green')

plt.show()
plt.clf()

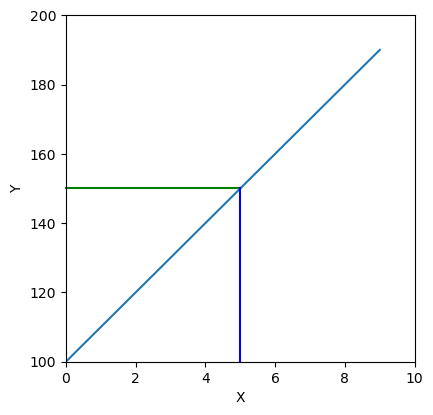
This code generate following plot:

Plot I want

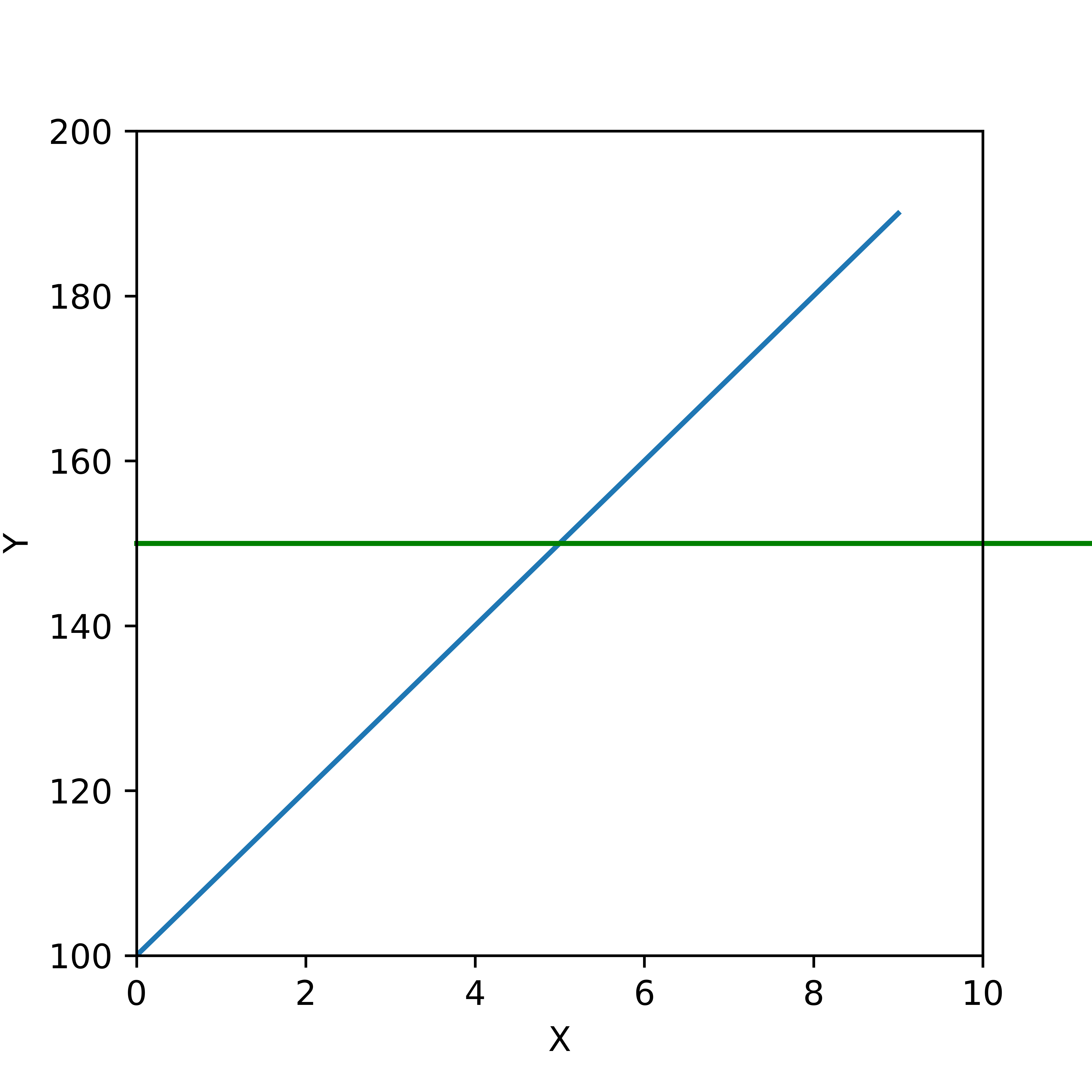
CodePudding user response：

I follow

CodePudding user response：

Li Yupeng's solution is great, here is an analytic solution using scipy's interpolate class:

from scipy.interpolate import interp1d

df = pd.DataFrame({'x': np.arange(10), 'y': np.arange(100, 200, 10)})

f = interp1d(df.y, df.x)
my_y_val = 150
my_x_val = float(f(my_y_val))

fig,ax = plt.subplots(figsize =(4.5,4.5))
ax.plot(df.x,df.y)

plt.xlabel('X')
plt.ylabel('Y')
plt.xlim(0,10)
plt.ylim(100,200)

my_y_max = (my_y_val - ax.get_ylim()[0])/(ax.get_ylim()[1] - ax.get_ylim()[0])
my_x_max = (my_x_val - ax.get_xlim()[0])/(ax.get_xlim()[1] - ax.get_xlim()[0])

ax.axhline(y=150, xmin=0, xmax=my_x_max, clip_on= False, color='green')
ax.axvline(x=float(my_x_val), ymin=0, ymax=my_y_max, clip_on= False, color='blue')

plt.show()
plt.clf()

We create a simple linear interpolation function based on our data (reversing input and output for this case), then find the appropriate value for our given x and plot it. Note that the values for ymax/ymin and xmax/xmin are in terms of a fraction of the Axes, not values on the x- and y-axes, so we need to calculate them, allowing for an axis not starting at 0 (as is the case for one of them here).

Of course you don't need a library to implement interpolation on a straight line, but you can swap in quadratic, linear, spline, etc as needed.