How to nearly connect two points with arc-like angled segments?-CodePudding

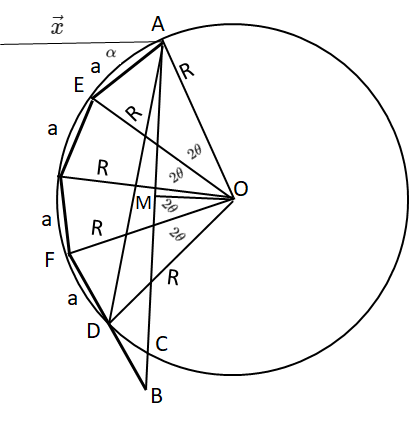
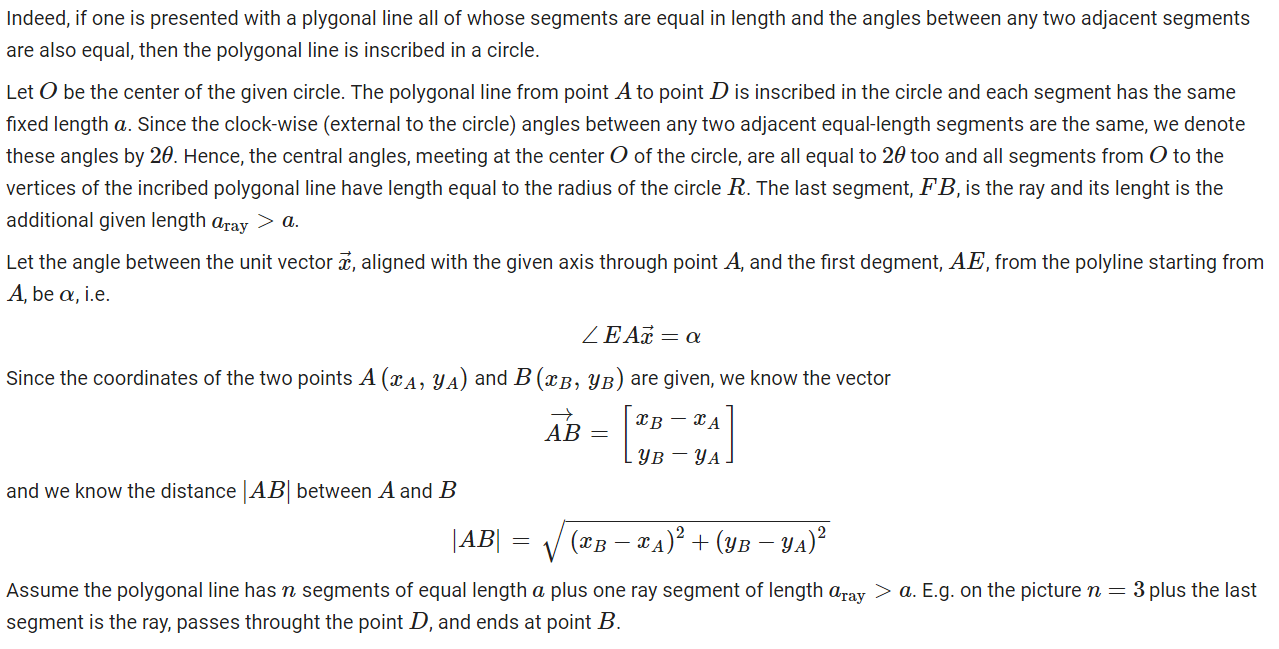Let's say we have two points in 2D space: A (center of blue square) and B (center of orange square). We are also given several fixed-sized lines as well as an infinite line (like a ray) with a minimal length. Furthermore we have a start-angle alpha for A.

Now how can we consecutively arrange the fixed-length lines starting at A and then the infinite line so that the angle of the first line is alpha and the infinite line exactly crosses B? Additionally there is one restriction:

The angles between two lines should be the same (this means many constellations of values make a solution impossible, but only ones with possible solutions are to be considered)

The result can look like this (in this sample with all segments having equal length). Imagine that a line stretched from the last segment (which represents the ray at its min-length) hits B.

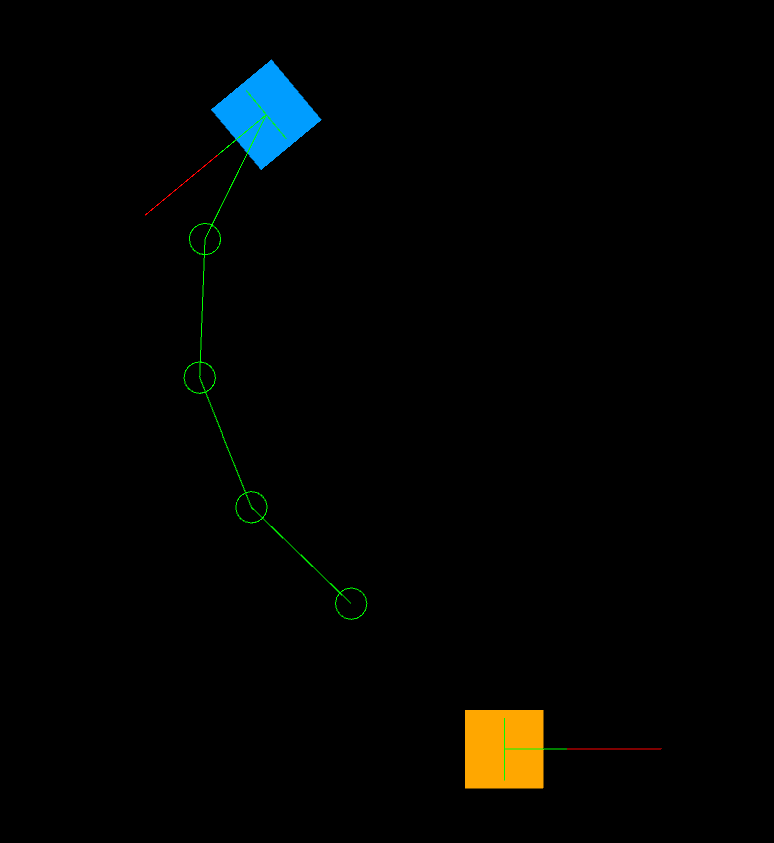
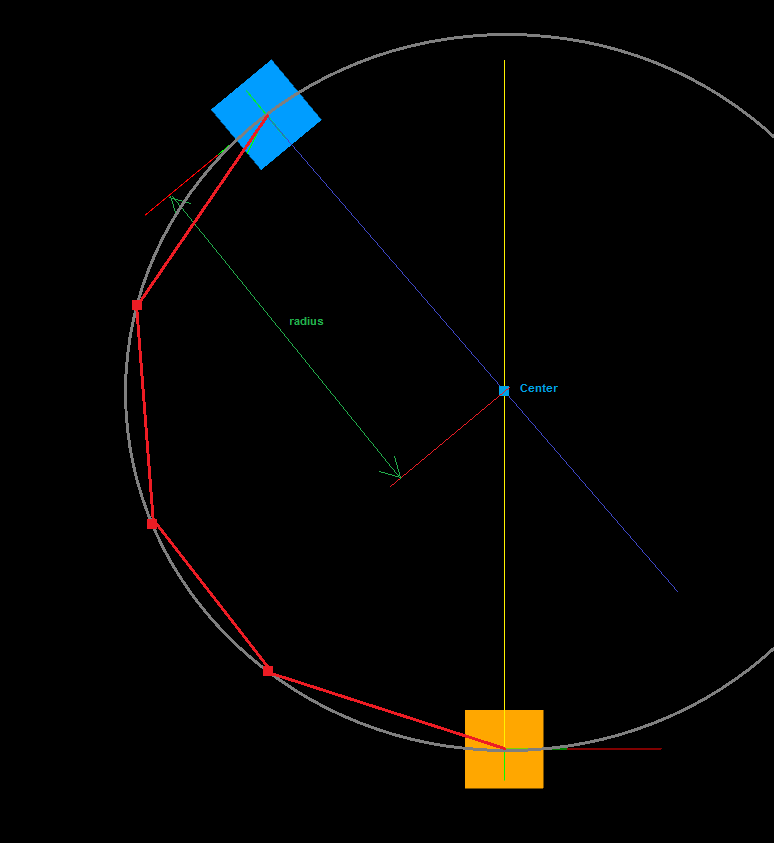
Now I have found a procedural solution by starting from A with 180° angles between the segments and checking whether a ray from the final segment hits B. Depending on which side of this ray, B lies, it re-starts from A with a decreased or increased angle until it overshoots the target. Then it halves the step-size and continues in the reverse direction until the next overshoot and so on. Eventually this ends when the steps have dropped below a threshold.

This image shows all the attempts of finding a semi accurate angle: 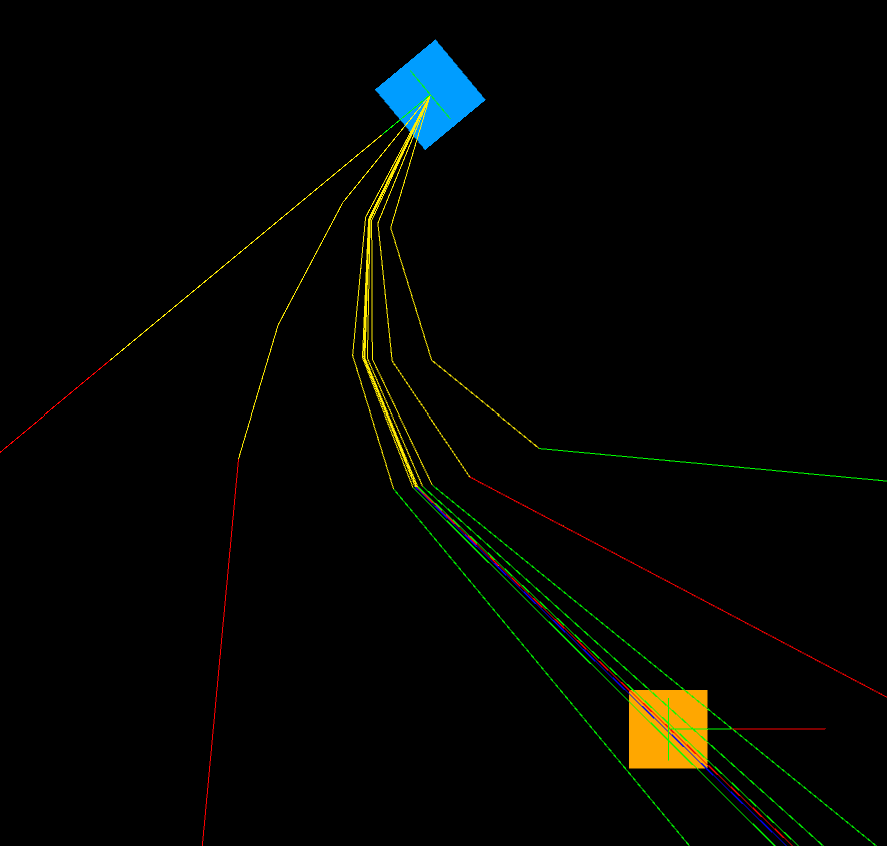The yellow segments are the limited-length ones and the other colors are the infinite rays (where blue is the solution).

Unfortunately this quickly gets computationally heavy when high accuracy is required.

There has to be a mathematical approach\solution to this, or not?

I have realized that this arc obviously is a segment of a circle and also that the origin of that circle has to be somewhere on a line from A at angle of alpha /-90° (so that the starting-line is a tangent of the circle and has exactly angle alpha). The problem now is, how to calculate the radius of this circle so that segments taken along points on its circumference have exactly the required length?

Hope someone has an idea. Huge thanks already!

For context if someone is interested: This is for a special type of "joint" in a physics simulation and for example to be used to make mesh-animated objects flexible and realistically bendable but NOT stretchable. Imagine a human spine for example.

That's why the segments have an enforced, fixed length and in practice, B is being forced to be at the end of the min-length of the ray-segment, however physics influence may pull it away slightly, so that it has to be corrected continuously. This solution shall yield better results than individual joints between the segments which can collapse in a zig zag in ugly ways. It already looks promising with the procedural computation solution if accuracy is high enough but it's not as performant as one expects from realtime simulations...

CodePudding user response：

If I understood the problem correctly, the solution seems to be calculable within one take, without iterative approximations like the one you have been implementing. Here is my take on the problem:

CodePudding user response：

So you are searching for circle that crosses both endpoints with defined tangents. So simple O(1) intersection between 2 axises will do:

cast ray/axis from each endpoint perpendicular to the tangent

so in 2D either use parametric circle equation with parameter as tangent /- 90deg or if you have direction vector swap x,y and negate one of them
find intersection of rays/axises (circle center (x0,y0) )

just google the equation or derive yourself of extract from here:
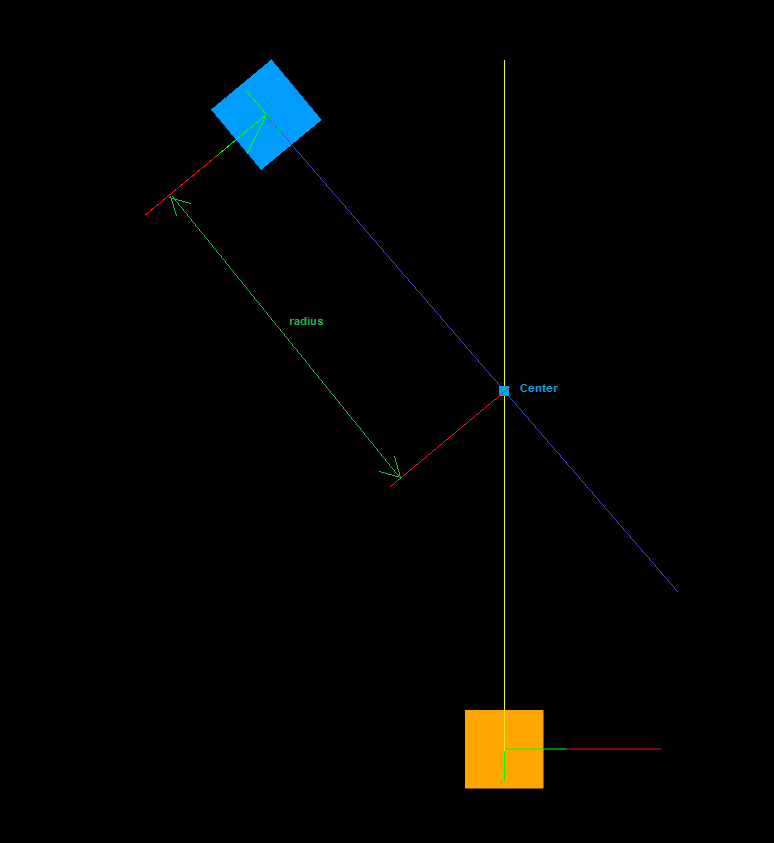
- compute start end angles for each endpoint
```
a = atan2(ay-y0,ax-x0);
b = atan2(by-y0,bx-x0);
```
- compute the missing points
```
c = a   (b-a)*(i/(n-1))
x(i) = x0   r*cos(c)
y(i) = y0   r*sin(c)
i = 0,1,2,3,...,n-1
```
  beware a,b might need small tweak in order to cover the correct part of circle (matching the tangents and avoidance of crossing 0/360 deg). Usual remedies are swapping a,b and or add/sub 360 deg to one of them. Based on the winding of the tangents and result of a<b ...

CodePudding user response：

Either by geometrical approach or by analytical approach, it would be possible to simplify the equation to be solved in iterations slightly. However it might be impossible to avoid resorting to numerical calculation in any manners.

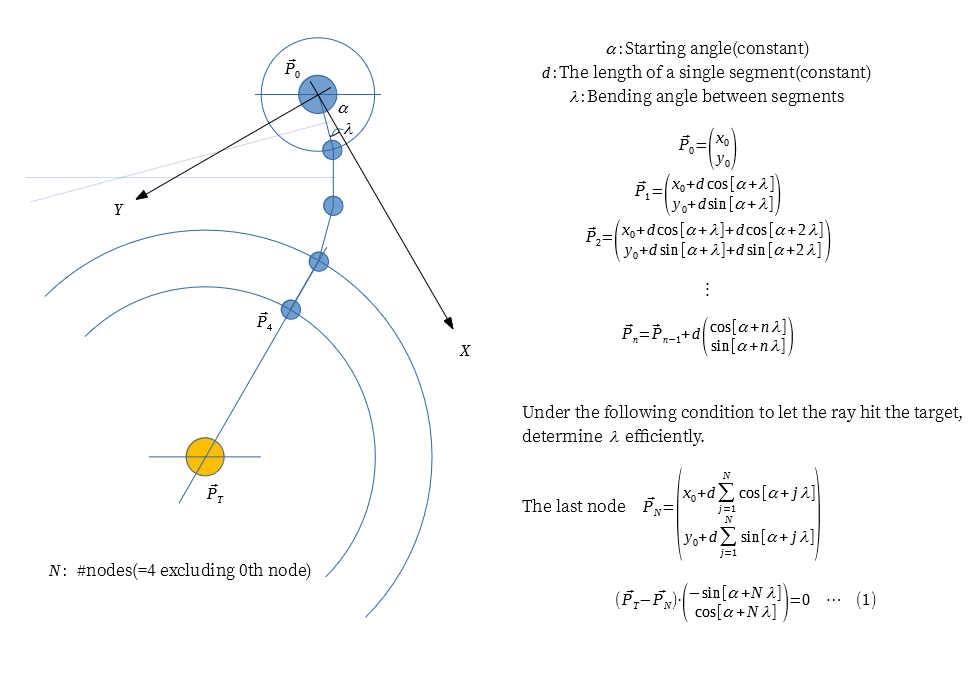
The original problem

To my understanding the original problem is summarized as follows:

Analytical solution

Though there is a geometry tag, but I'd like to show my analytical approach hereunder.

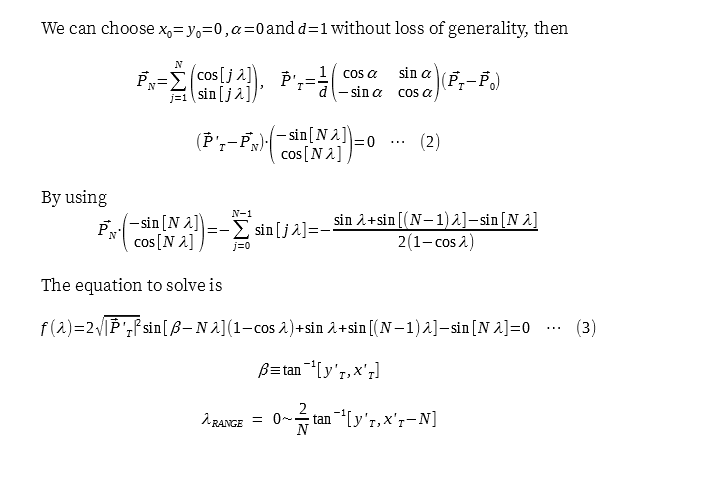Note: tan^(-1)[y, x] = atan2(y, x)

Though we could eliminate costly summation in the equation (2), however the final equation (3) cannot be solved analytically. Therefore we would still need to use bisection method or something within the appropriate range.