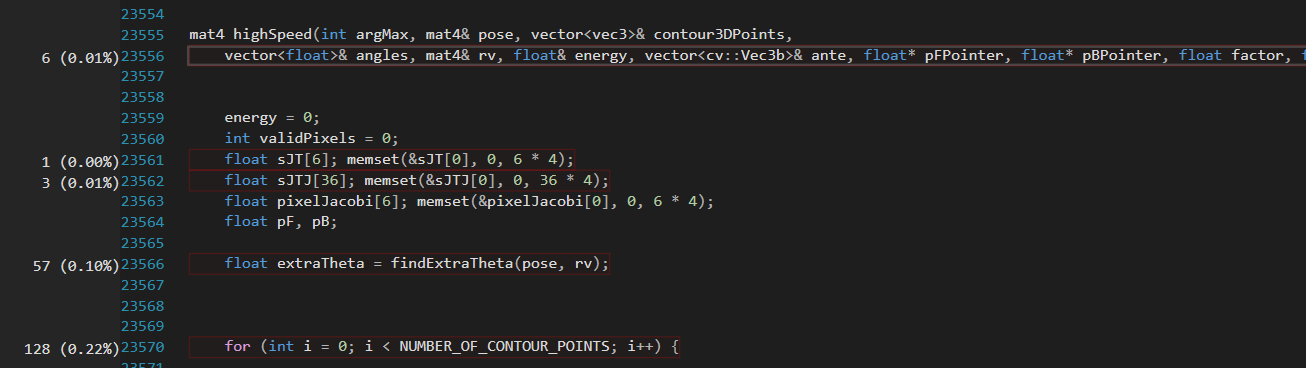
I'm using the Visual Studio profiler for the first time and I'm trying to interpret the results. Looking at the percentages on the left, I found this subtraction's time cost a bit strange:

Other parts of the code contain more complex expressions, like:

Even a simple multiplication seems way faster than the subtraction :

Other multiplications take way longer and I really don't get why, like this :

So, I guess my question is if there is anything weird going on here.

Complex expressions take longer than that subtraction and some expressions take way longer than similar other ones. I run the profiler several times and the distribution of the percentages is always like this. Am I just interpreting this wrong?

Update:

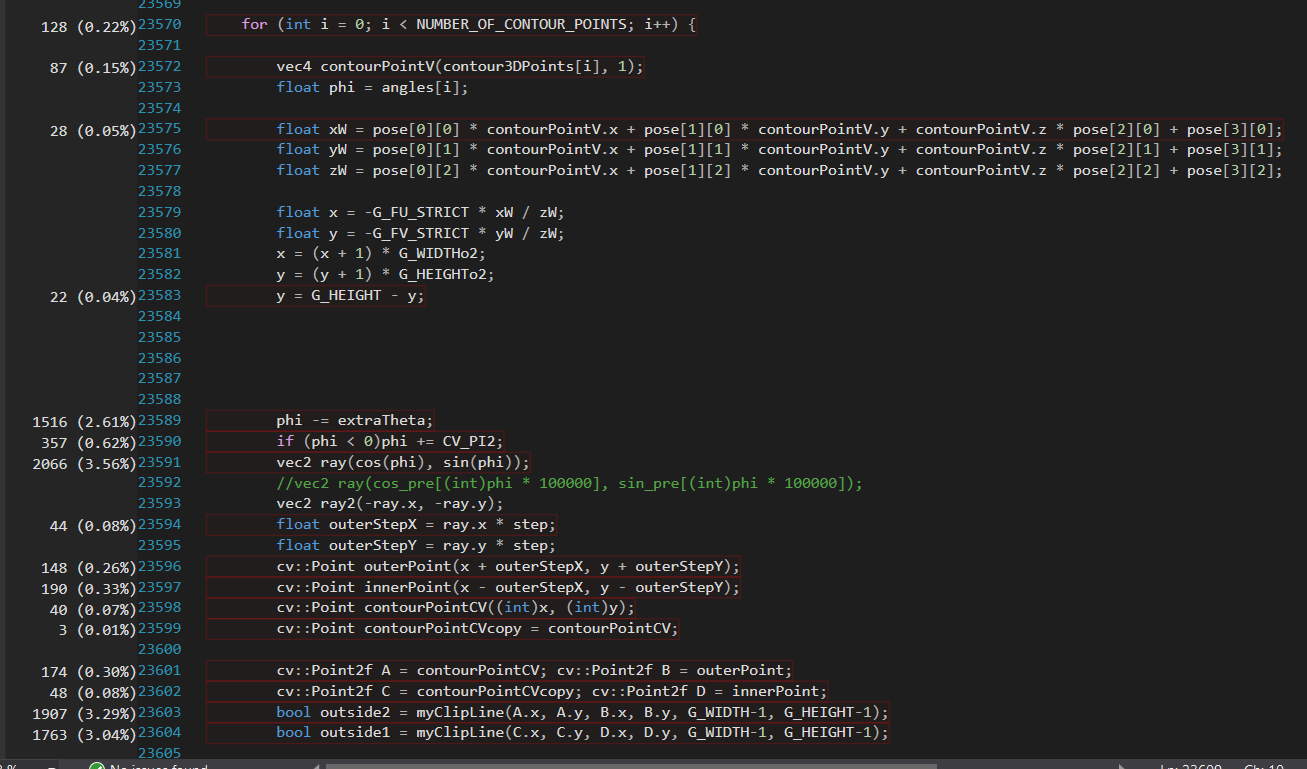
I was asked to give the profile for the whole function so here it is, even though it's a bit big. I ran the function inside a for loop for 1 minute and got 50k samples. The function contains a double loop. I include the text first for ease, followed by the pictures of profiling. Note that the code in text is a bit updated.

 for (int i = 0; i < NUMBER_OF_CONTOUR_POINTS; i  ) {

    vec4 contourPointV(contour3DPoints[i], 1);
    float phi = angles[i];

    float xW = pose[0][0] * contourPointV.x   pose[1][0] * contourPointV.y   contourPointV.z * pose[2][0]   pose[3][0];
    float yW = pose[0][1] * contourPointV.x   pose[1][1] * contourPointV.y   contourPointV.z * pose[2][1]   pose[3][1];
    float zW = pose[0][2] * contourPointV.x   pose[1][2] * contourPointV.y   contourPointV.z * pose[2][2]   pose[3][2];

    float x = -G_FU_STRICT * xW / zW;
    float y = -G_FV_STRICT * yW / zW;
    x = (x   1) * G_WIDTHo2;
    y = (y   1) * G_HEIGHTo2;
    y = G_HEIGHT - y;



    phi -= extraTheta;
    if (phi < 0)phi  = CV_PI2;
    int indexForTable = phi * oneKoverPI;
    //vec2 ray(cos(phi), sin(phi));
    vec2 ray(cos_pre[indexForTable], sin_pre[indexForTable]);
    vec2 ray2(-ray.x, -ray.y);
    float outerStepX = ray.x * step;
    float outerStepY = ray.y * step;
    cv::Point2f outerPoint(x   outerStepX, y   outerStepY);
    cv::Point2f innerPoint(x - outerStepX, y - outerStepY);
    cv::Point2f contourPointCV(x, y);
    cv::Point2f contourPointCVcopy(x, y);

    bool cut = false;
    if (!isInView(outerPoint.x, outerPoint.y) || !isInView(innerPoint.x, innerPoint.y)) {
        cut = true;
    }
    bool outside2 = true; bool outside1 = true;

    if (cut) {
        outside2 = myClipLine(contourPointCV.x, contourPointCV.y, outerPoint.x, outerPoint.y, G_WIDTH - 1, G_HEIGHT - 1);
        outside1 = myClipLine(contourPointCVcopy.x, contourPointCVcopy.y, innerPoint.x, innerPoint.y, G_WIDTH - 1, G_HEIGHT - 1);
    }


    myIterator innerRayMine(contourPointCVcopy, innerPoint);
    myIterator outerRayMine(contourPointCV, outerPoint);

    if (!outside1) {
        innerRayMine.end = true;
        innerRayMine.prob = true;
    }
    if (!outside2) {
        outerRayMine.end = true;
        innerRayMine.prob = true;
    }



    vec2 normal = -ray;
    float dfdxTerm = -normal.x;
    float dfdyTerm = normal.y;
    vec3 point3D = vec3(xW, yW, zW);
    cv::Point contourPoint((int)x, (int)y);



    float Xc = point3D.x; float Xc2 = Xc * Xc; float Yc = point3D.y; float Yc2 = Yc * Yc; float Zc = point3D.z; float Zc2 = Zc * Zc;
    float XcYc = Xc * Yc; float dfdxFu = dfdxTerm * G_FU; float dfdyFv = dfdyTerm * G_FU; float overZc2 = 1 / Zc2; float overZc = 1 / Zc;
    pixelJacobi[0] = (dfdyFv * (Yc2   Zc2)   dfdxFu * XcYc) * overZc2;
    pixelJacobi[1] = (-dfdxFu * (Xc2   Zc2) - dfdyFv * XcYc) * overZc2;
    pixelJacobi[2] = (-dfdyFv * Xc   dfdxFu * Yc) * overZc;
    pixelJacobi[3] = -dfdxFu * overZc;
    pixelJacobi[4] = -dfdyFv * overZc;
    pixelJacobi[5] = (dfdyFv * Yc   dfdxFu * Xc) * overZc2;


    float commonFirstTermsSum = 0;
    float commonFirstTermsSquaredSum = 0;

    int test = 0;
    while (!innerRayMine.end) {

        test  ;
        cv::Point xy = innerRayMine.pos(); innerRayMine  ;
        int x = xy.x;
        int y = xy.y;
        float dx = x - contourPoint.x;
        float dy = y - contourPoint.y;
        vec2 dxdy(dx, dy);

        float raw = -glm::dot(dxdy, normal);
        float heavisideTerm = heaviside_pre[(int)raw * 100   1000];
        float deltaTerm = delta_pre[(int)raw * 100   1000];


        const Vec3b rgb = ante[y * 640   x];
        int red = rgb[0]; int green = rgb[1]; int blue = rgb[2];
        red = red >> 3; red = red << 10; green = green >> 3; green = green << 5; blue = blue >> 3;
        int colorIndex = red   green   blue;

        pF = pFPointer[colorIndex];
        pB = pBPointer[colorIndex];
        float denAsMul = 1 / (pF   pB   0.000001);
        pF = pF * denAsMul;

        float pfMinusPb = 2 * pF - 1;
        float denominator = heavisideTerm * (pfMinusPb) pB   0.000001;
        float commonFirstTerm = -pfMinusPb / denominator * deltaTerm;

        commonFirstTermsSum  = commonFirstTerm;
        commonFirstTermsSquaredSum  = commonFirstTerm * commonFirstTerm;

    }
}

CodePudding user response：

Visual Studio profiles by sampling: it interrupts execution often and records the value of the instruction pointer; it then maps it to the source and calculates the frequency of hitting that line.

There are few issues with that: it's not always possible to figure out which line produced a specific assembly instruction in the optimized code.

One trick I use is to move the code of interest into a separate function and declare it with __declspec(noinline) .

In your example, are you sure the subtraction was performed as many times as multiplication? I would be more puzzled by the difference in subsequent multiplication (0.39% and 0.53%)

Update:

I believe that the following lines:

float phi = angles[i];

and

phi -= extraTheta;

got moved together in assembly and the time spent getting angles[i] was added to that subtraction line.