How to plot a symbolic function under specific intervals-CodePudding

I intend to plot the following function:

X = [x, y]
f = c'X   norm(c)* (sum(cos^2(X)) - sum(log(b-aX))
c = [7,2]
a = [2,3;4,6]
b = [10, 50]

So I want to get this

7x 2y 7.2*(cos^2(pi*x) cos^2(pi*y))-(log(10-2x-3y)  log(50-4x-6y) log(x) log(y))

How to plot the above function,when, let's say, -5<=x<=5 and -3<=y<=2?

I have tried the following:

import numpy as np
import matplotlib.pyplot as plt
from sympy import symbols
x,y = symbols(['x','y'])

c = np.array([7,2])                
A = np.array([[2,3],[4,6]])               
b = np.array([10,50])

So what to do next?? I don't know whether to use linspace??

plt.plot(A*x norm*(np.sum(np.cos^2(pi*x))-np.sum(log10(b-A*x))

CodePudding user response：

You can use sympy functions sympy.Function('cos')(x) and ('log')(x) and then lambdify. I didn't write down the exact function being too long but a simplified version works like this

import sympy
from sympy import *
from sympy.utilities.lambdify import lambdify, implemented_function
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm

if __name__=="__main__":
    
    x, y = symbols('x y')
    
    X = np.array([x,y])
    
    a = np.array([[2,3],[4,6]])
    b = np.array([10, 50])  # np.tile(b, (2,1))
    c = np.array([7, 2])
    
    fPart1 = sum(c*np.array( X ) )
    fPart2 = sum(np.array( c*np.array([sympy.Function('cos')(x) for x in X])))
    fPart3a = sum(c*np.array( sympy.Function('log')(sum(b - a[0,:]*X) )))
    fPart3b = sum(c*np.array( sympy.Function('log')(sum(b - a[1,:]*X) )))

    fPart3 = fPart3a   fPart3b

    
    zFunction = lambdify([x, y], fPart1   fPart2*fPart2   fPart3)

    xValues = np.linspace(-5, 5, 100)
    yValues = np.linspace(-3, 2, 100)
   
    X, Y = np.meshgrid(xValues, yValues)

    Z = zFunction(X, Y)

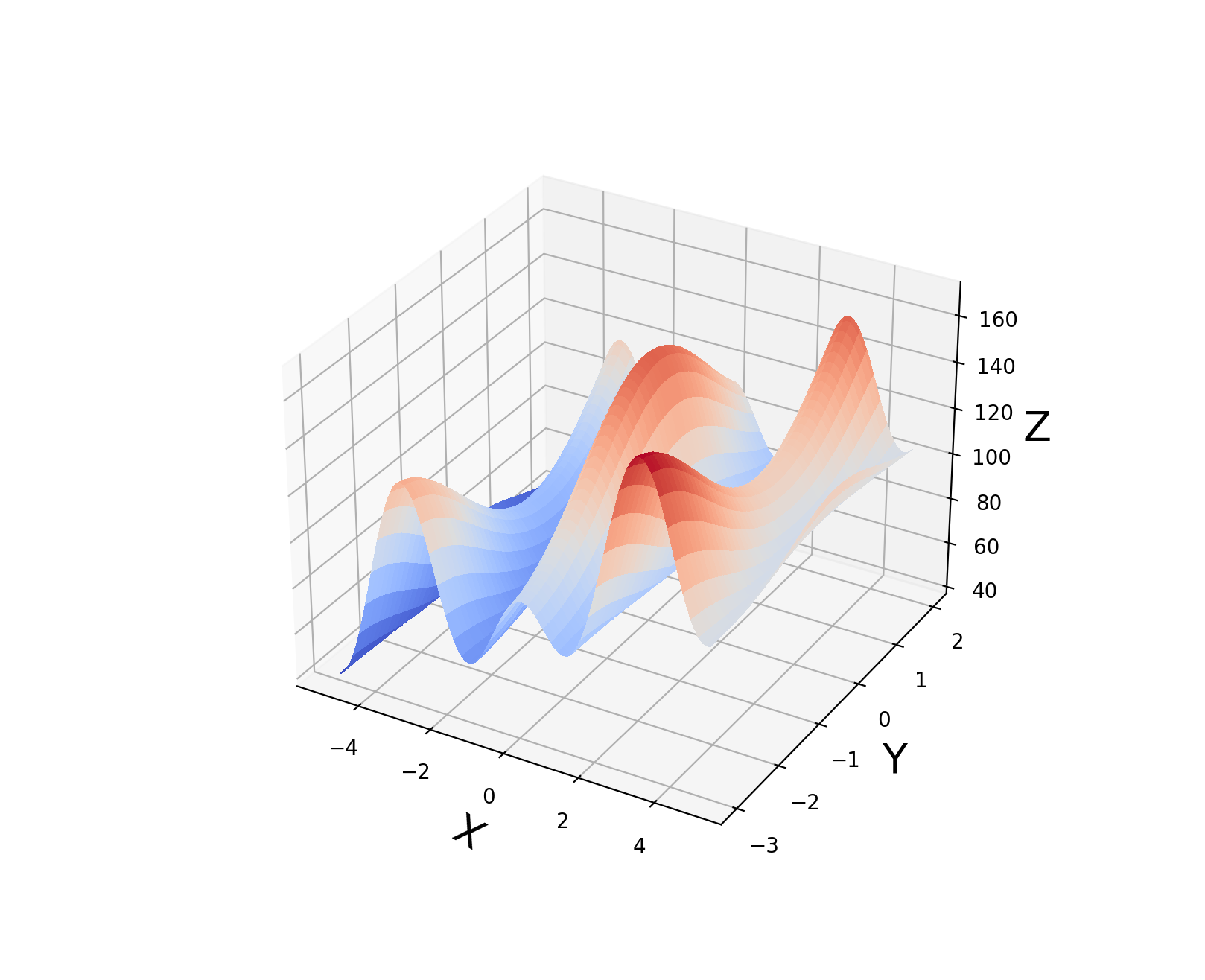
    fig, ax = plt.subplots(subplot_kw={"projection": "3d"})

    surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm, linewidth=0, antialiased=False)
    ax.set_xlabel('X', fontsize=20, rotation=150)
    ax.set_ylabel('Y', fontsize=20)
    ax.set_zlabel('Z', fontsize=20)

    plt.show()

Print the functions to know its what you want

In [4]: fPart1
Out[4]: 7*x   2*y

In [5]: fPart2
Out[5]: 7*cos(x)   2*cos(y)

In [6]: fPart3
Out[6]: 9*log(-4*x - 6*y   60)   9*log(-2*x - 3*y   60)