Get average of sub values in python nested dictionary-CodePudding

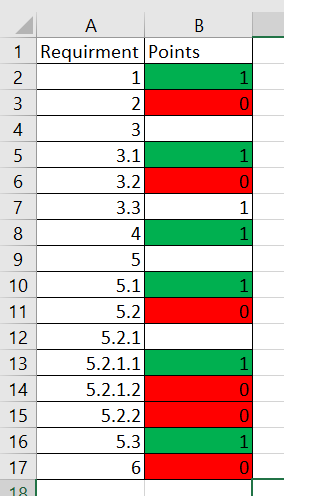
I have a situation where I have a table (imported from excel) wit requirments and sub requirments, it could be seen like this example:

 ------------- -------- 
| Requeriment | Points |
 ------------- -------- 
| 1           |        |
 ------------- -------- 
| 2           |        |
 ------------- -------- 
| 3           |        |
 ------------- -------- 
| 3.1         |        |
 ------------- -------- 
| 3.2         |        |
 ------------- -------- 
| 3.3         |        |
 ------------- -------- 
| 4           |        |
 ------------- -------- 
| 5           |        |
 ------------- -------- 
| 5.1         |        |
 ------------- -------- 
| 5.2         |        |
 ------------- -------- 
| 5.2.1       |        |
 ------------- -------- 
| 5.2.1.1     |        |
 ------------- -------- 
| 5.3         |        |
 ------------- -------- 
| 6           |        |
 ------------- --------

All requeriment max value is '1.0', if there are a case where the requirments have sub requirments, the requirments value = sum(subrequirments)/total subrequirments and it apply also to the sub requirments wit sub requirments.

Here I show how the requirments with no sub requirments are evaluated with a 0 if it is not complete and 1.0 if it is completed.

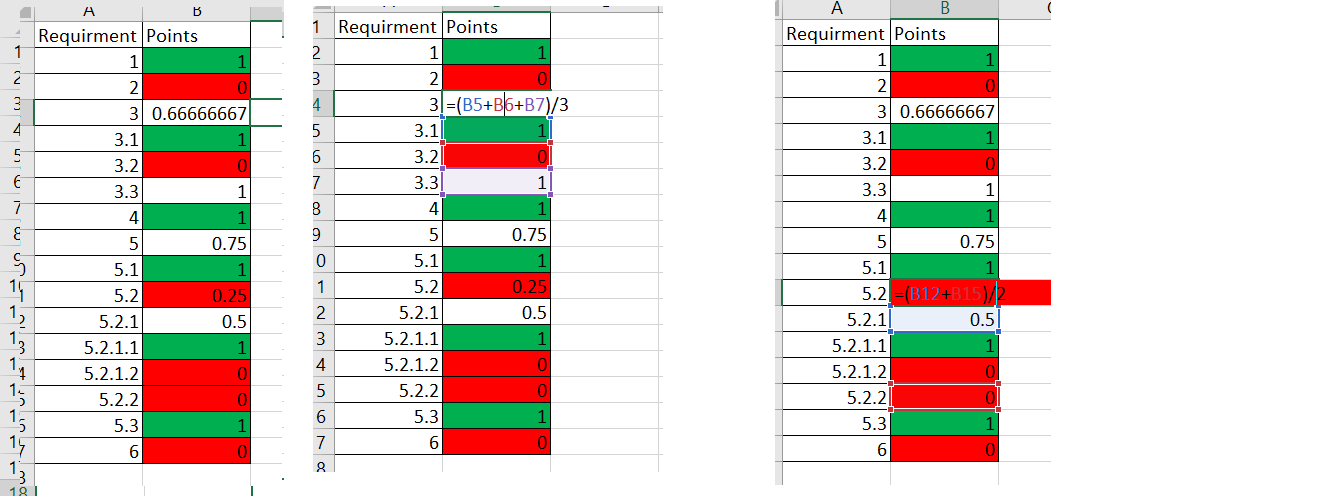
The requirments with sub requirments will be evaluated whith a formula: requeriment point = sum of sub requeriments/value of sub requeriments. the value will be some like this:

This table were converted in a dictionary like this:

{requeriments:{
 '1':{'points':'', subrequeriments: {}},
 '2':{'points':'', subrequeriments: {}},
 '3':{'points':'', subrequeriments: {
    '3.1':{'points':'', subrequeriments: {} },
    '3.2':{'points':'', subrequeriments: {} },
    '3.3':{'points':'', subrequeriments: {} }
   }
  },
 '4':{'points':'', subrequeriments: {}},
 '5':{'points':'', subrequeriments: {
    '5.1':{'points':'', subrequeriments: {} },
    '5.2':{'points':'', subrequeriments: {
      '5.2.1':{'points':'', subrequeriments: {
         '5.2.1.1':{'points':'', subrequeriments: {}
         }

        } 
      },
    '5.3':{'points':'', subrequeriments: {} }
   }
  },
 '6':{'points':'', subrequeriments: {}}
 }
}

At the end I can not get a good way to evaluate the requirments aplying the function requirment value = sum(subrequirments)/total subrequirments in the nested sub requirments.

Do you know a good way to aply it to a dictionary or at least a good way do do it to a lost or a table?

CodePudding user response：

Use a recursive function:

def calcPoints(d):
    points = 0
    for k,v in d.items():
        if v['points'] == '':
            v['points'] = calcPoints(v['subrequirements'])
        points  = float(v['points'])
    return str(points / max(1,len(d)))

Input:

data = {'requeriments': 
{'1': {'points': '1', 'subrequirements': {}}, 
 '2': {'points': '0', 'subrequirements': {}}, 
 '3': {'points': '', 'subrequirements': 
    {'3.1': {'points': '1', 'subrequirements': {}},
     '3.2': {'points': '0', 'subrequirements': {}},
     '3.3': {'points': '1', 'subrequirements': {}}}}, 
 '4': {'points': '1', 'subrequirements': {}}, 
 '5': {'points': '', 'subrequirements': 
    {'5.1': {'points': '1', 'subrequirements': {}},
     '5.2': {'points': '', 'subrequirements': 
          {'5.2.1': {'points': '', 'subrequirements': 
                  {'5.2.1.1': {'points': '1', 'subrequirements': {}}, 
                   '5.2.1.2': {'points': '0', 'subrequirements': {}}}}, 
           '5.2.2': {'points': '0', 'subrequirements': {}}}},
     '5.3': {'points': '1', 'subrequirements': {}}}}, 
 '6': {'points': '0', 'subrequirements': {}}}}

Output:

calcPoints(data['requeriments']) # '0.5694444444444444'

print(data)

{'requeriments': 
 {'1': {'points': '1', 'subrequirements': {}}, 
  '2': {'points': '0', 'subrequirements': {}}, 
  '3': {'points': '0.6666666666666666', 'subrequirements': 
     {'3.1': {'points': '1', 'subrequirements': {}}, 
      '3.2': {'points': '0', 'subrequirements': {}}, 
      '3.3': {'points': '1', 'subrequirements': {}}}}, 
  '4': {'points': '1', 'subrequirements': {}}, 
  '5': {'points': '0.75', 'subrequirements': 
     {'5.1': {'points': '1', 'subrequirements': {}}, 
      '5.2': {'points': '0.25', 'subrequirements': 
           {'5.2.1': {'points': '0.5', 'subrequirements': 
                   {'5.2.1.1': {'points': '1', 'subrequirements': {}}, 
                    '5.2.1.2': {'points': '0', 'subrequirements': {}}}}, 
            '5.2.2': {'points': '0', 'subrequirements': {}}}}, 
      '5.3': {'points': '1', 'subrequirements': {}}}}, 
  '6': {'points': '0', 'subrequirements': {}}}}