I want to calculate the overlap of two binomial distributions A and B (e.g.

• A with 100 trials and a probability of success with 0.7
• B with 100 trials and a probability of success with 0.6.)

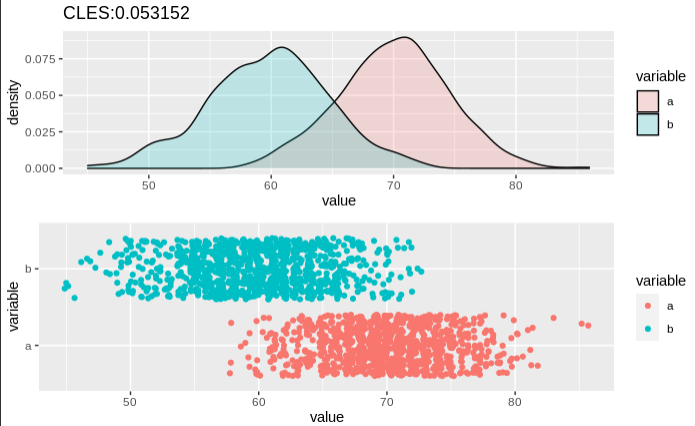
I think I can empirically get the value (see 2. picture) by simulating values and calculating the "Common Language Effect Size" (how many points of B are bigger than A). Since the overlap only depends on the probability of success and the number of trials, it feels like there should be a direct solution without simulating it first.

Is there a direct way to get to this value in R?

.

CodePudding user response：

Get the probability density of the 0.6 binomial for each possible outcome that it can be larger (1 through 100) and multiply it by the CDF of the 0.7 binomial for the same outcome minus one, then sum all the products:

> sum(pbinom(0:99, 100, 0.7)*dbinom(1:100, 100, 0.6))
[1] 0.05896353

Check the answer against a simulation:

> mean(rbinom(1e6, 100, 0.6) > rbinom(1e6, 100, 0.7))
[1] 0.058982