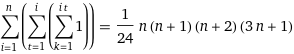What is the time complexity (big O) of this function ? and how to calculate it ?

I think it's O(N^3) but am not sure.

int DAA(int n){
    int i, j, k, x = 0;
    for(i=1; i <= n; i  ){
        for(j=1; j <= i*i; j  ){
            if(j % i == 0){
                for(k=1; k <= j; k  ){
                    x  = 10;
                }
            }
        }
    }
    return x;
}

CodePudding user response：

The complexity is O(n^4)

But not because you blindly drop unused iteration.

it's because when you consider all instruction, O(n n^3 n^4) = O(n^4)

int DAA(int n){
   int x = 0;
   for(int i=1; i <= n; i  ) // O(n)
      for(int j=1; j <= i*i; j  ) // O(1 2 ...n^2) = O(n^3)
         if(j % i == 0) // O(n^3) same as loop j
            for(int k=1; k <= j; k  ) // O(n^4), see below
               x  = 10; // O(n^4) same as loop k

   return x;
}

Complexity of conditioned inner loop

the loop k only execute when j%i==0, i.e. {i, i*2, i*3 ... i*i}

so for the case the inner-most loop execute, the algorithm is effectively

int DAA(int n){
   int x = 0;
   for(int i=1; i <= n; i  ) // O(n)
      for(int t=1; t <= i; t  ) // O(1 2 ... n) = O(n^2)
         for(int k=1; k <= t*i; k  ) // O(n^4)
               x  = 10;
   return x;
}

Why simply drop unused iteration not work?

let's say it's now

int DAA(int n){
   int x = 0;
   for(int i=1; i <= n; i  ) // O(n)
      for(int j=1; j <= i*i; j  ) // O(1 2 ... n^2) = O(n^3)
         if(j == i) 
            for(int k=1; k <= j; k  )
               x  = 10; // oops! this only run O(n^2) time

   return x;
}
// if(j==i*log(n)) also cause loop k becomes O((n^2)log(n))
// or, well, if(false) :P

Although the innermost instruction only run O(n^2) time. The program actually do if(j==i)(and j , j<=i*i) O(n^3) time, which make the whole algorithm O(n^3)

CodePudding user response：

Time complexity can be easier to compute if you get rid of do-nothing iterations. The middle loop does not do anything unless j is a multiple of i. So we could force j to be a multiple of i and eliminate the if statement, which makes the code easier to analyze.

int DAA(int n){
    int x = 0;
    for(int i=1; i <= n; i  ){
        for(int m=1; m <= i; m  ){  // New variable to avoid the if statement
            int j = m*i;            // The values for which the inner loop executes
            for(int k=1; k <= j; k  ){
                x  = 10;
            }
        }
    }
    return x;
}

The outer loop iterates n times. O(n) so far.

The middle loop iterates 1 time, then 2 times, then... n times. One might recognize this setup from the O(n²) sorting algorithms. The loop executes n times, and the number of iterations increases to n, leading to O(n×n) complexity.

The inner loop is executed on the order of n×n times (the complexity of the middle loop). The number of iterations for each execution increases to n×n (the maximum value of j). Similar to how the middle loop multiplied its number of executions and largest number of iterations to get its complexity, the complexity of the inner loop – hence of the code as a whole – should become O(n⁴), but I'll leave the precise proof as an exercise.

The above does assume that the time complexity represents the number of times that x = 10; is executed. That is, it assumes that the main work of the innermost loop overwhelms the rest of the work. This is usually what is of interest, but there are some caveats.

The first caveat is that adding 10 is not overwhelming more work than incrementing. If the line x = 10; is not a convenient stand-in for "do work", then it might be that the time complexity should include all iterations, even those that do no work.

The second caveat is that the condition in the if statement is cheap relative to the innermost loop. In some cases, the conditional might be expensive, so the time complexity should include the number of times the if statement is executed. Eliminating the if statement does interfere with this.

If you happen to fall into one of these caveats, you'll need a count of what was omitted. The modified code omits i²−i iterations of the middle loop on each of its n executions. So the omitted iterations would contribute n times n²−n, or O(n³) towards the overall complexity.

Therefore, the complexity of the original code is O(n⁴ n³), which is the same as O(n⁴).