Breadth First Traversal in Haskell-CodePudding

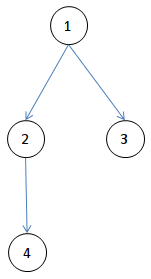
I need to find all the paths in a tree-like structure.

I recently defined Deep First traversal (or iterate) as follows:

dfIterate:: (a -> [a]) -> a -> [[a]]
dfIterate f a = map (a:) ([] : concatMap (dfIterate f) (f a))

It takes a seed a and a function a -> [a] (from each "a", you can get to multiple a's). The result is a list of paths starting from the seed. It works well:

ghci> let f a = if a == 1 then [2, 3] else if a == 2 then [4] else []
ghci> dfIterate f 1
[[1],[1,2],[1,2,4],[1,3]]

My function dfIterate iterates correctly and shows me all the paths. The function f simulates the tree above.

But how to make a "Breadth First Traversal"? The result in this case should be: [[1],[1,2],[1,3],[1,2,4]]. My first attempt:

bfIterate :: (a -> [a]) -> [a] -> [[a]]
bfIterate _ [] = [[]]
bfIterate f (a:as) = map (a:) (bfIterate f (as    (f a)))

I tried to use the second argument as a queue. I know I'm quite far from the result... Thanks

EDIT: This link gives interesting lines of approach: Breadth-First Search using State monad in Haskell. However, my question is about finding all paths (i.e. [[a]]), while that question is for finding single solutions (i.e. [a])

CodePudding user response：

Correctness first, efficiency later.

bfPaths :: (a -> [a]) -> a -> [[a]]
bfPaths step seed  =  go [ (seed, [seed]) ]
 where
 go []  =  []
 go ((s, path) : q) = path :
   go (q    [ (x, path    [x]) | x <- step s ])

indeed maintaining a queue and adding the nodes to it, level by level.

Trying it:

> bfPaths f 1
[[1],[1,2],[1,3],[1,2,4]]

Now you can look for ways to make it more efficient.