How to highlight the lowest curve (envelope) among multiple curves in matplotlib-CodePudding

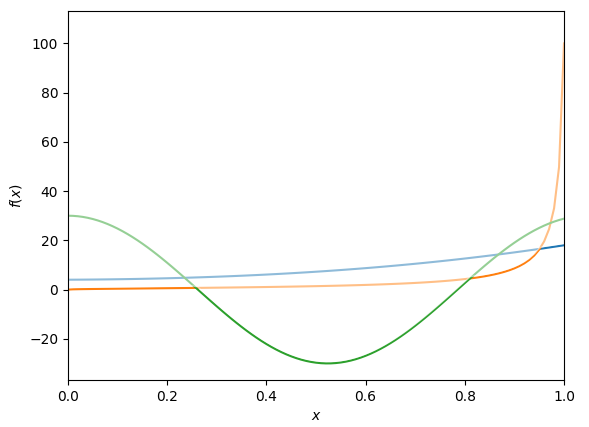
Say I have multiple math functions f1, f2, f3 represented by Python functions. I want to plot them together on the domain of [0, 1]. Here is what it looks like

import numpy as np
import matplotlib.pyplot as plt
import math

def f1(x):
    return 4*x**3   9*x**2   x   4
def f2(x):
    return math.sqrt(x) / (1.01 - x)
def f3(x):
    return 30 * math.cos(6 * x)

x = np.arange(0.0, 1.01, 0.01)
for f in [f1, f2, f3]:
    vecf = np.vectorize(f)
    y = vecf(x)
    plt.plot(x, y)
plt.xlim([0, 1])
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.show()

However, I want to highlight all lowest curve segments (i.e. the envelope) by using alpha = 1, while using alpha = 0.5 for other parts of the curves. I want to keep the color of each curve. The expected plot looks something like this:

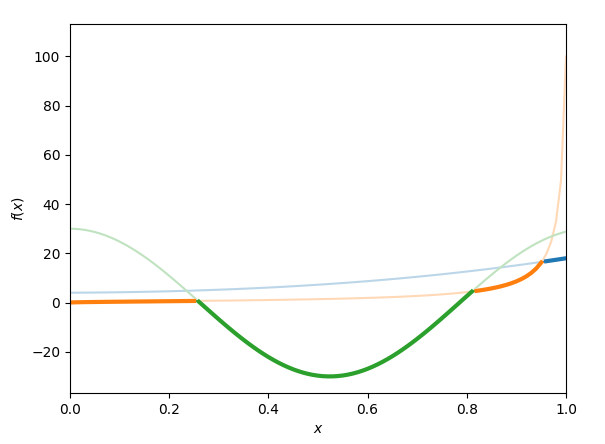
Can anyone suggest how to achieve this in matplotlib?

CodePudding user response：

I had a shot at doing what I suggested in the comments ("to just plot all curves, then compute a series that is effectively the minimum of the others combined and plot that as well, but with a 100% transparant line colour and shading the entire area above it in partially opaque white.") and I think it's pretty close to what you need:

import numpy as np
import matplotlib.pyplot as plt
import math

def f1(x):
    return 4*x**3   9*x**2   x   4
def f2(x):
    return math.sqrt(x) / (1.01 - x)
def f3(x):
    return 30 * math.cos(6 * x)

x = np.arange(0.0, 1.01, 0.01)
# initialise min_y to all infinite, there is probably a more efficient way to do this
min_y = np.inf * np.ones(x.shape)
for f in [f1, f2, f3]:
    vecf = np.vectorize(f)
    y = vecf(x)
    # zorder=0 to push curves below plane 
    plt.plot(x, y, zorder=0)
    # compute min_y as we go
    min_y = np.minimum(y, min_y)

# what you need, although the  1 is a bit arbitrary
# you may want to add some amount relative to the plt.ylim()
plt.fill_between(x, min_y 1, plt.ylim()[1], color='white', alpha=.5)

plt.xlim([0, 1])
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.show()

Result:

Maybe you want an alpha more like .7 or so, judging from your example.

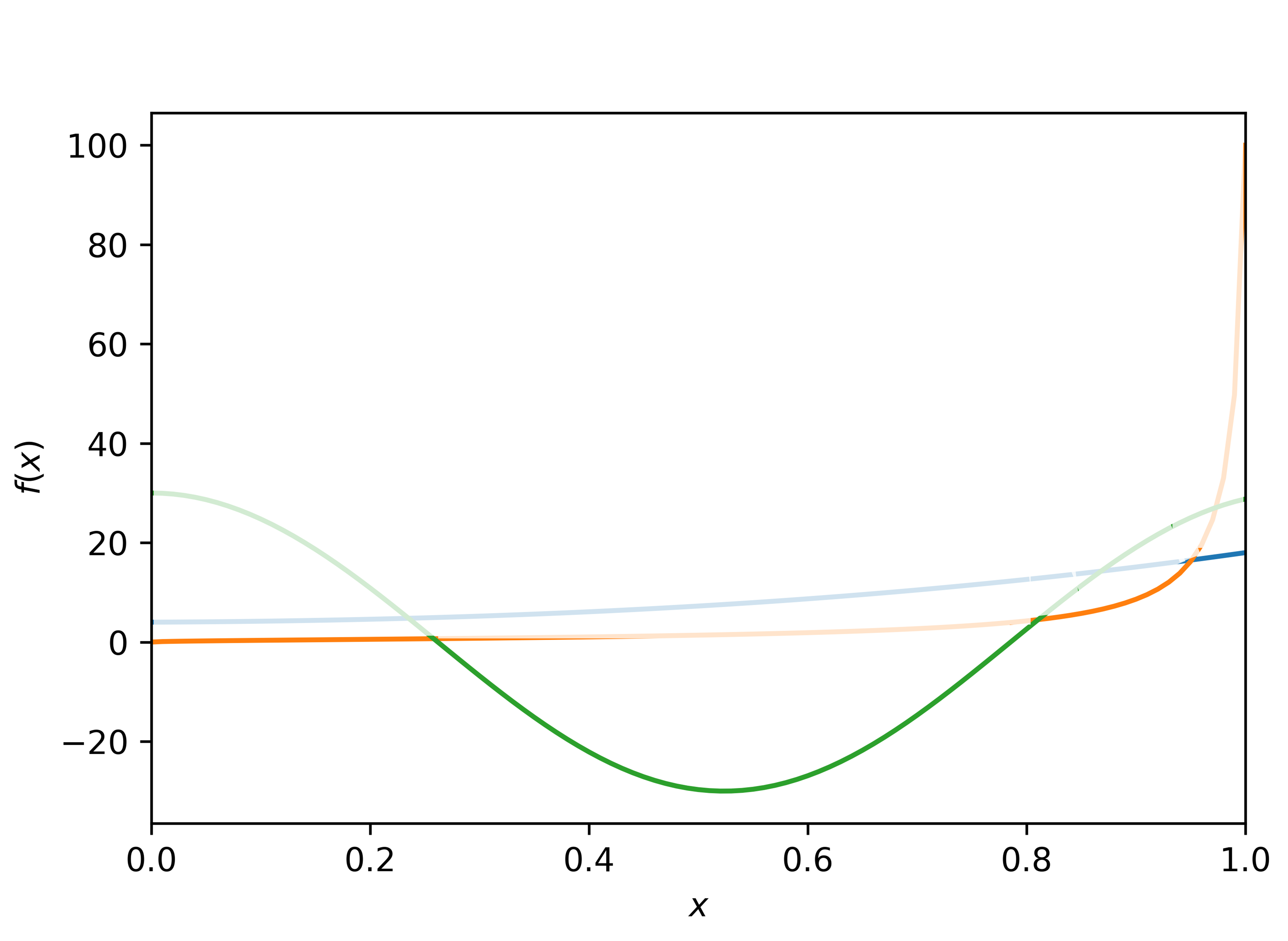
Sneaky follow-up question, to also make the lines fat:

import numpy as np
import matplotlib.pyplot as plt
import math

def f1(x):
    return 4*x**3   9*x**2   x   4

def f2(x):
    return math.sqrt(x) / (1.01 - x)

def f3(x):
    return 30 * math.cos(6 * x)

x = np.arange(0.0, 1.01, 0.01)
# initialise min_y to all infinite, there is probably a more efficient way to do this
min_y = np.inf * np.ones(x.shape)
plotted = []
for f in [f1, f2, f3]:
    vecf = np.vectorize(f)
    y = vecf(x)
    # zorder=0 to push curves below plane
    p = plt.plot(x, y, zorder=0)
    # compute min_y as we go
    min_y = np.minimum(y, min_y)
    # keep the plotted data, to reuse when plotting fat lines
    plotted.append((y, p[0].get_color()))

for y, c in plotted:
    plt.plot(x, np.ma.masked_where(y > min_y, y), color=c, zorder=1, linewidth=3)

# what you need, although the  1 is a bit arbitrary - you may want to add some amount relative to the plt.ylim()
plt.fill_between(x, min_y 1, plt.ylim()[1], color='white', alpha=.7)

plt.xlim([0, 1])
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.show()

Result: