I'm wondering if there's a way to quickly calculate the number of shared neighbors between any pairs of nodes (i.e., the number of nodes connected to both node i and j) from an adjacency matrix (like the one below) and then return the output in matrix format?

I've referenced these following posts,

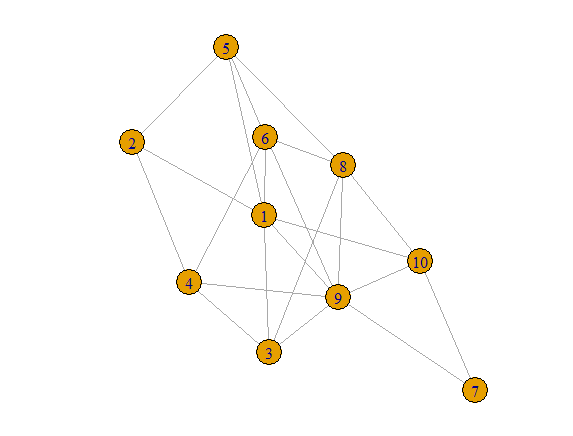
Notice for example that Shared[1,4] = 4. That is because nodes 1 and 4 have four shared neighbors,
Nodes 2,3,6 and 9. Shared[5,7]=0 because nodes 5 and 7 have no neighbors in common.

CodePudding user response：

I think @G5W's solution is super concise already, highly recommended!

Below is a graph theory way to solve it, maybe not that efficient:

> nb <- neighborhood(g,mindist = 1)

> outer(nb, nb, FUN = Vectorize(function(a, b) length(intersect(a, b))))
      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
 [1,]    6    1    1    4    2    2    2    5    3     1
 [2,]    1    3    2    0    1    3    0    1    2     1
 [3,]    1    2    4    1    2    4    1    1    3     3
 [4,]    4    0    1    4    2    1    1    3    2     1
 [5,]    2    1    2    2    4    2    0    1    3     2
 [6,]    2    3    4    1    2    5    1    2    3     3
 [7,]    2    0    1    1    0    1    2    2    1     1
 [8,]    5    1    1    3    1    2    2    5    3     1
 [9,]    3    2    3    2    3    3    1    3    7     3
[10,]    1    1    3    1    2    3    1    1    3     4

> t(adjm) %*% adjm
      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
 [1,]    6    1    1    4    2    2    2    5    3     1
 [2,]    1    3    2    0    1    3    0    1    2     1
 [3,]    1    2    4    1    2    4    1    1    3     3
 [4,]    4    0    1    4    2    1    1    3    2     1
 [5,]    2    1    2    2    4    2    0    1    3     2
 [6,]    2    3    4    1    2    5    1    2    3     3
 [7,]    2    0    1    1    0    1    2    2    1     1
 [8,]    5    1    1    3    1    2    2    5    3     1
 [9,]    3    2    3    2    3    3    1    3    7     3
[10,]    1    1    3    1    2    3    1    1    3     4