So I am looking at a problem which is similar in principle to computing partitions for a large N. My problem is similar to the following hypothetical problem.

Let's say that I have a random variable X which has possible outcomes of 1,2,..., 10, each of which occurs with corresponding probabilities P1,P2,...,P10. My hypothetical problem: if I generate 20 random and independent samples of X and sum them together, what is the likelihood of the resulting summations of 10,11,12,... 200.

A few approaches which occurred to me which are workable-in-theory but computationally-not-close-to-possible are as follows.

Idea 1) List out the partitions of 200. Remove any partition categories which use a number greater than 10. Calculate the probabilities of each and sum up for each sum (sum = 10,11,...,200). This is ezpz for small N, completely and totally bonkers for 'huge in this context' N like 200.

Idea 2) List out all the possible 20 item sample results (ie 1-1-1-1-1-1-1-1-1-2,1-1-1-1-1-1-1-1-1-2,etc), note the probability of each, and sum up for each sum (sum = 10, 11, ... , 200). Again, ezpz for small N, completely infeasible in this context.

I also had the following idea, but I was not able to get it to work. Idea 3) Modify your favorite 'generate the partitions' algorithm so that any number greater than 10 cannot be used in a partition. Similar to Idea 1 in principle, however we generate a small list and don't have to trim down a huge list. My two issues with this idea, a) I am not sure how to do this for any partition generation algorithm, and b) even if I could I am not convinced it would be computationally feasible.

Any points on how I can tackle this? At the end of the day it is similar to any host of other problems in the bucket of [enumerate all possible outcomes, compute the probability of each, aggregate the probabilities for each aggregate sum, and you have your answer]. However the sample space is so huge.

This would be really easy to approximate via monte carlo, but that approach leaves a bad taste in my mouth as so many of the theoretically possible outcomes will not show up, even 10 billion iterations or so.

Any thoughts on how to tackle this?

[I am flexible on the language of choice, but I have a bias towards using Python where possible]

CodePudding user response：

randomly generate 100000, and count each value apparend.If you want specific value, use binomial distribution. Here is a python simulation:

def random_int_by_probas_sum(probas_cum, r):
    """
    @param probas_cum cumulation probablities of the 10 random numbers.
    @param r random number
    return the value of r-percentage. for example r=0.3, it will return 3, r=0.8, it will return 8
    """
    for index in range(len(probas_cum)):
        if r <= probas_cum[index]:
            return index

import numpy as np
import pandas as pd
import random

nums = np.arange(0, 10, 1)
#
probas = [0.05, 0.15, 0.07, 0.13, 0.09, 0.11, 0.08, 0.12, 0.04, 0.16]
probas_cum = [0.05, 0.2, 0.27, 0.4, 0.49, 0.6, 0.68, 0.8, 0.84, 1]
random_count = 1000000
sums = []

for _ in range(random_count):
    sum_step = 0
    for i in range(10):
        r = random.random()
        sum_step  = random_int_by_probas_sum(probas_cum, r)
    sums.append(sum_step)

sums = pd.Series(sums)
sums.value_counts()

CodePudding user response：

Wrote a recursive solution based on the idea in Aaron's comment. This uses the solution for previous values of N to find larger values of N.

Unlike the other answer, this method is not an approximation.

import itertools
from collections import defaultdict, namedtuple

numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
probs = [0.1] * 10
Distribution = namedtuple('Distribution', 'numbers probs')


def find_prob(dist, n=1):
    if n == 0:
        # If you draw 0 numbers, you have a 100% change of getting zero.
        return Distribution([0], [1])
    else:
        # Find probability of each number, drawing one fewer sample
        dist_b = find_prob(dist, n - 1)
        # Combine two distributions. Add up all probabilities for getting
        # the same number.
        prob_for_num = defaultdict(float)
        for a, p_a in zip(dist.numbers, dist.probs):
            for b, p_b in zip(dist_b.numbers, dist_b.probs):
                num = a   b
                # Probability of p(A&B) = p(A) * p(B)
                prob = p_a * p_b
                prob_for_num[num]  = prob

        # Split numbers and probabilities into two lists
        numbers, probs = zip(*prob_for_num.items())
        return Distribution(numbers=numbers, probs=probs)
sol = find_prob(Distribution(numbers=numbers, probs=probs), 20)

I set this up in a simple way, with each number 1 through 10 having equal probability. The numbers don't have to be consecutive, though, and the probabilities don't need to be equal. I just did that for the sake of simplicity.

It can easily sum up with N=20. It starts to slow down at around N=1000. If you want to sum up more samples than this, you may want to look into more efficient methods of recursion.

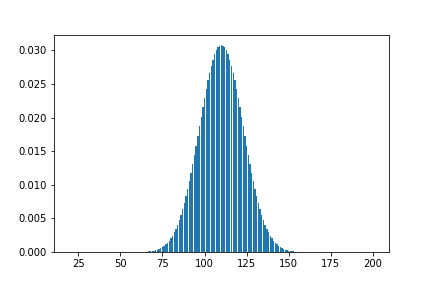
When I sum up 20 samples of a uniform distribution, I get this graph of probabilities:

...which is the normal distribution, as expected.