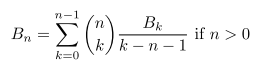I want to write a bernoulli function bernoulli:: Integer -> Rational in haskell, using the following algorithm for calculating the bernoulli number for a given integer.

the functions "frac" and "binom" are used to calculate the binomial in the definition. this is what i have so far:

fact :: Integer -> Integer
fact i = foldr (*) 1 [1..i]

binom :: Integer -> Integer -> Integer
binom n k = (fact n) `div` (fact k* fact (n-k))

bernoulli :: Integer -> Rational
bernoulli 0 = 1
bernoulli i = ((binom i j) * (bernoulli j)) / (j - i - 1) where j = i-1

I've tried it a few different times now, but either the recursion doesn't work or the resulting Rational is wrong.

CodePudding user response：

I found three problems in your code:

1. Parentheses in the binom
2. Mixing Rational and Integer
3. Your function bernoulli is not a sum, but only first member

In my code, you can see how I coped with these problems.

fact :: Integer -> Integer
fact i = foldr (*) 1 [1..i]

binom :: Integer -> Integer -> Integer
binom n k = (fact n) `div` ((fact k) * fact (n-k))

bernoulli :: Integer -> Rational
bernoulli 0 = 1
bernoulli n = sum [
    toRational(binom n k) * (bernoulli k) / toRational(k - n - 1)
    | k <- [0..(n-1)]
  ]

Test:

map bernoulli [0..10]

Output:

[1 % 1,(-1) % 2,1 % 6,0 % 1,(-1) % 30,0 % 1,1 % 42,0 % 1,(-1) % 30,0 % 1,5 % 66]

Small addition:
If we don't follow the rule of leveraging existing libraries, the solution could also look like this:

binom :: Rational -> Rational -> Rational
binom n k = product [ ( n   1 - i ) / i | i <- [ 1 .. k ] ]

bernoulli :: Rational -> Rational
bernoulli 0 = 1
bernoulli n = sum [
    binom n k * bernoulli k / (k - n - 1)
    | k <- [0..(n-1)]
  ]

Because:

Note the similarity of the program with mathematical notation.

p.s. bernoulli with foldr:

bernoulli :: Integer -> Rational
bernoulli n = foldr (summand n) (0::Rational) [0 .. (n-1)]
  where
    summand n k s1 = s1   toRational(binom n k) * bernoulli k / toRational(k - n - 1)