How to plot the graph using MATLAB (or not matlab))?-CodePudding

I've got the function fi(ϕ)=γi sin(2⋅sinϕ) for i=1,2 where γ1=0.01 and γ2=0.02

ϕ1(0)=0.1 and ϕ2(0)=0.2

ϕ1/dt=f1(ϕ) d⋅sin(ϕ2−ϕ1)

ϕ2/dt=f2(ϕ) d⋅sin(ϕ1−ϕ2)

where d=0.1

So there should be something like for example this table:

t     | ϕ1  | ϕ2
0.00  | 0.1 |0.2
0.01  | ... |...
0.02  | ... |...
...
100.00| ... | ...

And so using the received values it's needed to plot a graph by the coordinates

So the question is how to plot the function ϕ2(ϕ1) on the the following graph using MATLAB?

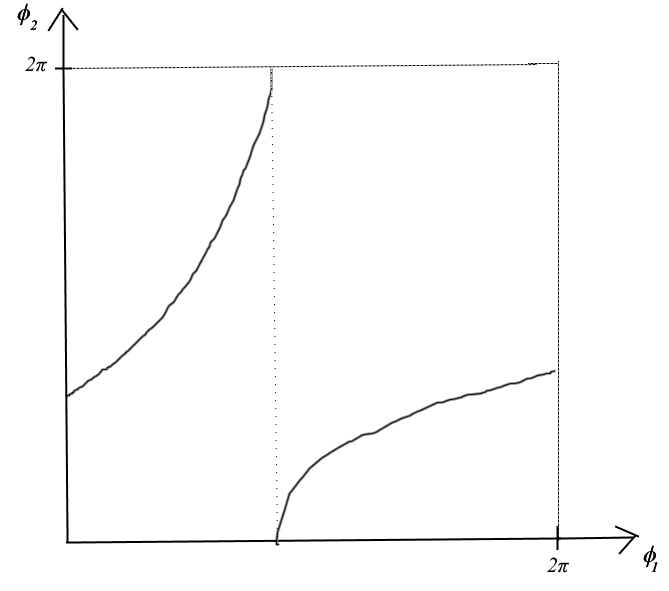
CodePudding user response：

So the story of the system might be that you start with two uncoupled and slightly different equations

ϕ1/dt=f1(ϕ1)
ϕ2/dt=f2(ϕ2)

and connect them with a coupling or exchange term sin(ϕ2-ϕ1),

ϕ1/dt=f1(ϕ1) d⋅sin(ϕ2−ϕ1)
ϕ2/dt=f2(ϕ2) d⋅sin(ϕ1−ϕ2)

In a matlab script you would implement this as

y0 = [ 0.1; 0.2 ];
[T,Y] = ode45(eqn,[0, 100], y0);

plot(Y(:,1),Y(:,2));

function dy_dt = eqn(t,y)
  d = 0.1;
  g = [ 0.01; 0.02 ];
  f = g sin(2*sin(y));
  exch = d*sin(y(2)-y(1));
  dy_dt = f [d;-d];
end%function

which gives almost a diagonal line ending at [pi; pi]. With a stronger coupling constant d this becomes slightly more interesting.

You can give the parameters as parameter arguments, then you have to declare them via odeset in an options object, or use anonymous functions to bind the parameters in the solver call.