Boost chi2square inversion-CodePudding

The Boost inversion_chi_square_distribution shared different value than chi2inv from Matlab, Input parameters(1 - 1e-3, 2).

Can someone explain what i did wrong ?

I used the gamma inversion distribution.

Example :

inputs :

shape param : n/2 
scale : 2
p = 1 - 1e-3;

Matlab -> chi2inv(1-1e-3, 2);

Matlab -> gaminv(1-12-3, n/2, 2);

Result -> 13.8155. The same result for both functions.

C Boost

cdf(boost::math::inverse_gamma_distribution<double> (n/2,2), a); -> a = 1-1e-3; n = 2;

Result : 0.13506461276045323

Thank you in advance.

CodePudding user response：

Not knowing much about the maths/statistics side, I can guess that Matlab's idea of gaminv is the special function, not a distribution.

According to Wolfram Alpha you should probably be using the "inverse regularized gamma function":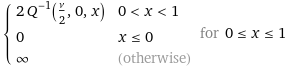

Or in plaintext:

ConditionalExpression[Piecewise[{{2 InverseGammaRegularized[ν/2, 0, x], 0 < x < 1}, {0, x <= 0}}, Infinity], 0 <= x <= 1]

I don't immediately know how to apply this idea to candidate code - but it was too large to post in a comment

CodePudding user response：

Boost implements inverse-gamma distribution, whereas you need the inverse cumulative distribution function (icdf) of the standard gamma distribution. The former is the gamma distribution calculated at 1/x, whereas the latter is the inverse of the cdf for the gamma distribution, see https://en.wikipedia.org/wiki/Quantile_function . You use two completely different functions with similar names, hence different results.

I'm afraid the function you need does not have a closed form in a general case (though, for example, for shape = 1 scale = 2 it is easy to derive its closed form: -2.0*log(1.0 - x)). One can implement it using some numerical inversion scheme, like bisection, Newton etc.