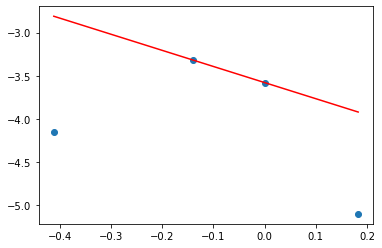
I'm trying to fit a linear model to a set of data, with the constraint that all the residuals (model - data) are positive - in other words, the model should be the "best overestimate". Without this constraint, linear models can be easily found with numpy's polyfit as shown below.

import numpy as np
import matplotlib.pyplot as plt

x = [-4.12179107e-01, -1.40664082e-01, -5.52301563e-06,  1.82898473e-01]
y = [-4.14846251, -3.31607886, -3.57827245, -5.09914559]

plt.scatter(x,y)
coeff = np.polyfit(x,y,1)
plt.plot(x,np.polyval(coeff,x),c='r',label='numpy-polyval')
plt.plot(x,np.polyval([-2,-3.6],x),c='g',label='desired-fit') #a rough guess of the desired result
plt.legend()

See e.g.

CodePudding user response：

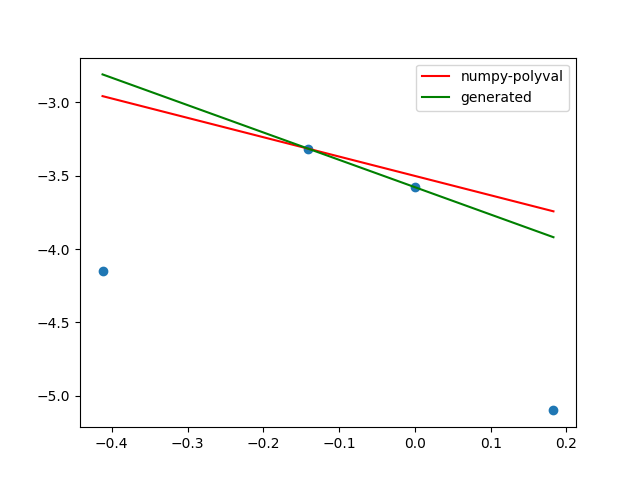
Interesting problem. The line through the top two points is a poor choice. It is not always a feasible solution (points can be above this line). It only works well for uncorrelated variables (makes sense, there is little information about the optimal slope in the two highest points). A shifted fit is would appear to be a good heuristic.