Create Tree Structure using Pandas-CodePudding

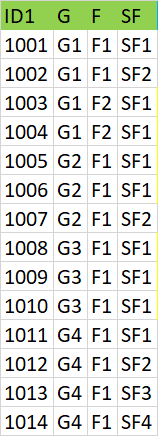
I need to generate a new column based on the unique combinations in the data below

import pandas as pd

df = pd.DataFrame({'ID': [1001, 1002, 1003, 1004,1005,1006,1007,1008,1009,1010,1011,1012,1013,1014],
                   'G': ['G1','G1','G1','G1', 'G2','G2','G2', 'G3','G3','G3', 'G4','G4','G4','G4',],
                   'F': ['F1','F1', 'F2','F2','F1','F1','F1','F1','F1','F1','F1','F1','F1','F1',],
                   'SF': ['SF1', 'SF2', 'SF1','SF1','SF1','SF1','SF2','SF1','SF1','SF1','SF1','SF2','SF3','SF4']
                  }
                )
df

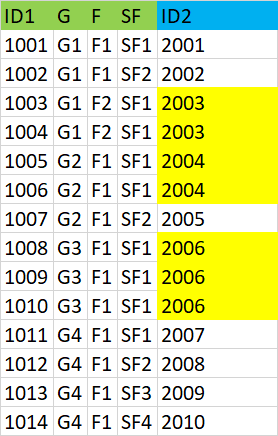
As per the below table, columns G,F,SF will have unique combinations for every value in column ID1. For every unique combination a new column(ID2) must be generated at the end

Sample output is below

However, am trying to achieve this via SQL, want to check if this can be done using Pandas.

CodePudding user response：

The logic is not fully clear, but assuming you forgot the 2004 and you want to increment when there is a non-duplicate, you could do:

cols = ['G', 'F', 'SF']
# global duplicates
df['ID2'] = (~df[cols].duplicated()).cumsum().add(2000)

# consecutive duplicates
df['ID3'] = df[cols].ne(df[cols].shift()).any(1).cumsum().add(2000)

NB. it is also unclear whether you want to consider global or consecutive duplicates (both result in the same on the provided dataset), I proposed a solution for both cases (ID2 and ID3, respectively).

output:

      ID   G   F   SF   ID2   ID3
0   1001  G1  F1  SF1  2001  2001
1   1002  G1  F1  SF2  2002  2002
2   1003  G1  F2  SF1  2003  2003
3   1004  G1  F2  SF1  2003  2003
4   1005  G2  F1  SF1  2004  2004
5   1006  G2  F1  SF1  2004  2004
6   1007  G2  F1  SF2  2005  2005
7   1008  G3  F1  SF1  2006  2006
8   1009  G3  F1  SF1  2006  2006
9   1010  G3  F1  SF1  2006  2006
10  1011  G4  F1  SF1  2007  2007
11  1012  G4  F1  SF2  2008  2008
12  1013  G4  F1  SF3  2009  2009
13  1014  G4  F1  SF4  2010  2010