I have a few polygons in 3d space (given as loops of vertices and edges), but they lay on the same plane. I need to find a bridges between "holes" and "polygon":
grey - polygon
red - bridges

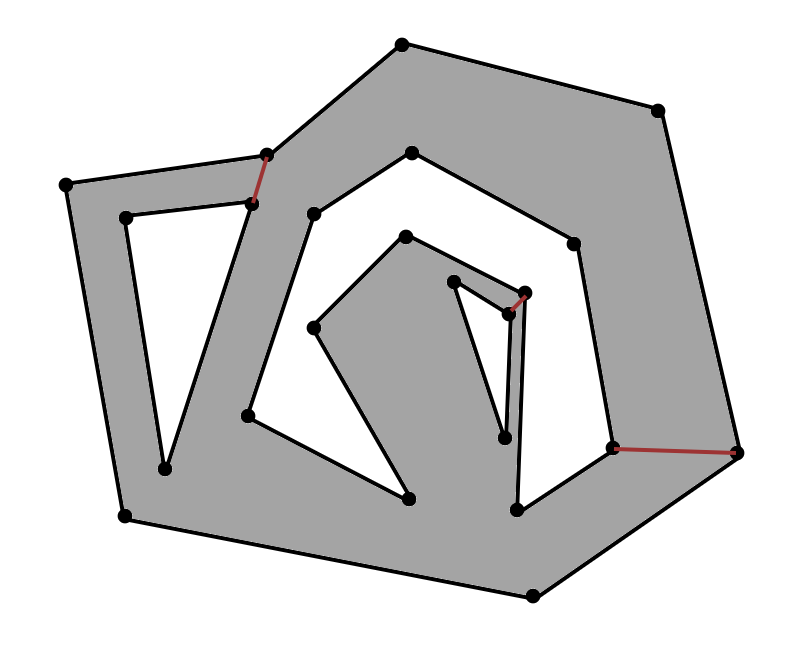
Does somebody know the algorithm to find such bridges for the polygon, if they are contained as a tree: polygon as a parent and it contains all holes as children elements?


I have found this material (4. finding mutually visible vertices): https://www.geometrictools.com/Documentation/TriangulationByEarClipping.pdf
but I don't know how to apply this method to the program if the coordinates are given in 3D.

CodePudding user response：

first see:

• How can I connect two parallel 2d polygons to create a seamless 3d mesh?

its similar task so it might get you some inspiration.

After some thinking you could try simple brute force:

1. definitions

   let polygon points be stored in p[] array and hole points in h[] array.

2. try every combination if bridge edge between p[] and h[]

   such that it does not intersect any previous edge not any of the polygons. In case of intersection use shorter edge and remove the longer ones.

3. remove non "parallel" bridges

   above solution should lead to triangulated like polygon with holes so we need to remove all edges but one that share the same point so:

   1. sort edges by used first point (index)
   2. remove all lines that share the same first point leave the smallest one
   3. sort edges by used second point (index)
   4. remove all lines that share the same second point leave the smallest one

In code the first 2 bullets would look like this:

int i,j,k,e;
line l;
List<point> p,h; // input points
List<line>  P,H; // input polygon and holes lines
List<line>  B;   // output bridge lines

for (i=0;i<p.size;i  )
 for (j=0;j<h.size;j  )
   {
   l=line(p[i],h[j]); e=0;
   // first test if new edge l intersects P,H
   if (!e) for (k=0;k<P.size;i  ) if (intersekt(l,P[k])){ e=1; break; }
   if (!e) for (k=0;k<H.size;i  ) if (intersekt(l,H[k])){ e=1; break; }
   // if not test if intersect already found bridges
   if (!e) for (k=0;k<B.size;i  ) if (intersekt(l,B[k]))
     {
     if (l.length()<=B[k]) B.del(k); // remove bigger edge from B
      else { e=1; break; }           // or throw away l for good
     }
   if (!e) B.add(l);
   } 

Beware I have not test this just wrote the code directly in Answer editor so it might need some tweaking especially the last loop (maybe you will have to find first if l should be deleted or not and only then remove edges from B ...

CodePudding user response：

If you need to find just any bridge without any optimization, then the solution for a simple polygon with a single hole would be simple:

• Step 1. Find a vertex v1of the hole polygon with maximal value of the y-coordinate.
• Step 2. Find a vertex v2 of the outer polygon with minimal value of the y-coordinate, greater than the y-coordinate of the vertex v1, found previously.
• Step 3. Connect vertices v1 and v2 by a bridge.

Of course, the maximization/minimization of the y-coordinate is not your only choice - you can choose any direction, along which you'll be able to perform the search, described above.

This solution won't work in case you have many holes, because they can conceal each other. Even more - there might be cases, where you won't be able to find a bridge between a concealed hole and the outer polygon. However, you can apply the algorithm, described above, to finding bridges between holes - in this case you'll need to analyze location of holes relative to each other. For example, you'll need to (algorithmically) find that the smallest hole on your picture is bounded from above by the biggest hole, so this algorithm will easily give you a bridge between them.