The scaling of my plots make the curves appear the same when they are not. How to shape them so that-CodePudding

I have placed my two plots side by side. However, I have noticed that the plots have been shaped to be the same size, and this has caused the distribution curves to appear the same when I know they are not. The Cobalt curve should be shorter and fatter than the Rhodium curve.

fig, (ax1, ax2) = plt.subplots(1, 2)

mu = Mean_Sd(rhodium_data, "Mean all Angles")[2]
sigma = Mean_Sd(rhodium_data, "Mean all Angles")[3] 
x = mu   sigma * np.random.randn(437)

num_bins = 50

n, bins, patches = ax.hist(x, num_bins, density=1) # creates histogram

# line of best fit
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))

#Creating the plot graphic
ax1.plot(bins, y, '-')
ax1.tick_params(top=True, right=True)
ax1.tick_params(direction='in', length=6, width=1, colors='0')
ax1.grid()
ax1.set_xlabel("Mean of the Four Angles")
ax1.set_ylabel("Probability density")
ax1.set_title(r"Rhodium Distribution")

#####-----------------------------------------------------------------------------------####

mu = Mean_Sd(cobalt_data, "Mean all Angles")[2]
sigma = Mean_Sd(cobalt_data, "Mean all Angles")[3] 
x = mu   sigma * np.random.randn(437)

num_bins = 50

n, bins, patches = ax.hist(x, num_bins, density=1) # creates histogram

# line of best fit
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))

#Creating the plot graphic
ax2.plot(bins, y, '-')
ax2.tick_params(top=True, right=True)
ax2.tick_params(direction='in', length=6, width=1, colors='0')
ax2.grid()
ax2.set_xlabel("Mean of the Four Angles")
ax2.set_ylabel("Probability density")
ax2.set_title(r"Cobalt Distribution")

####----------------------------------------------------------------------------------####

fig.tight_layout()
plt.show()

Here is my code. I'm working with Python 3 on Jupyter Notebooks.

Edit

The mean of 'Mean all Angles' from 'Cobalt Data' is 105.1 Degrees. The standard deviation of 'Mean all Angles' from column 'Cobalt Data' is 7.866 Degrees.

The mean of 'Mean all Angles' from 'Rhodium Data' is 90.19 Degrees. The standard deviation of 'Mean all Angles' from column 'Rhodium Data' is 1.35 Degrees.

mu will be the mean, and sigma is the standard deviation.

Rhodium: mu = 90.19. sigma = 1.35 Cobalt: mu = 105.1. sigma = 7.866

CodePudding user response：

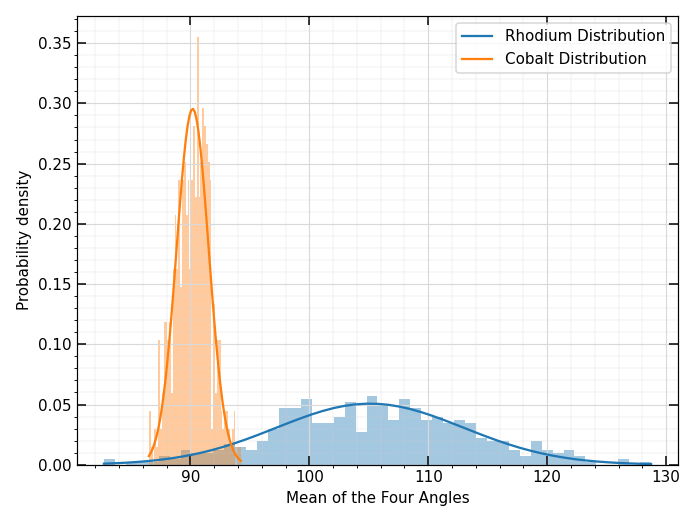
As you have pointed out, the range difference between the two distributions is substantial. You could try to set ax1.set_xlim, ax1.set_ylim, ax2.set_xlim, ax2.set_ylim, but in my opinion at least one subplot would end up to be hardly legible.

What if you combine the two subplots into one?

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots(1)

mu = 105.1
sigma = 7.866
x1 = mu   sigma * np.random.randn(437)

num_bins = 50

n, bins1, patches = ax.hist(x1, num_bins, density=1, color="tab:blue", alpha=0.4) # creates histogram

# line of best fit
y1 = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins1 - mu))**2))

#####-----------------------------------------------------------------------------------####

mu = 90.19
sigma = 1.35
x2 = mu   sigma * np.random.randn(437)

num_bins = 50

n, bins2, patches = ax.hist(x2, num_bins, density=1, color="tab:orange", alpha=0.4) # creates histogram

# line of best fit
y2 = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins2 - mu))**2))

#Creating the plot graphic
ax.plot(bins1, y1, '-', label="Rhodium Distribution", color="tab:blue")
ax.plot(bins2, y2, '-', label="Cobalt Distribution", color="tab:orange")
ax.set_xlabel("Mean of the Four Angles")
ax.grid()
ax.set_ylabel("Probability density")
ax.tick_params(top=True, right=True)
ax.tick_params(direction='in', length=6, width=1, colors='0')
ax.legend()
ax.grid(which='major', axis='x', linewidth=0.75, linestyle='-', color='0.85')
ax.grid(which='minor', axis='x', linewidth=0.25, linestyle='--', color='0.80')
ax.grid(which='major', axis='y', linewidth=0.75, linestyle='-', color='0.85')
ax.grid(which='minor', axis='y', linewidth=0.25, linestyle='--', color='0.80')
ax.minorticks_on()

####----------------------------------------------------------------------------------####

fig.tight_layout()
plt.show()