Plot big dataset clusters in python-CodePudding

So basically I'm kind of new to sklearn and ML with python in general. I'm used to RapidMiner and other GUI tools. I have this dataset with over 2 million rows and 5 columns, which are my Principal Components (around 98% variance). I executed the clustering with kmeans and obtained the labels. I already know that the number of clusters has to be 4, and initialized the algorithm using kmeans generated centroids.

from sklearn.cluster import KMeans
preds = KMeans(n_clusters=4, init=centers_init).fit_predict(sc_norm_pca_data)
result = np.append(sc_norm_pca_data, preds.reshape([2208556, 1]), axis=1) # append labels to data

Now I'm facing 2 problems:

I don't know what's the best way to visualize the data since the number of components are 5. Maybe I can do a 3D plot using the first 3 PCs or take the labels and attach them to the pre-PCA dataset instead.
I tried to plot the results on a bidimensional plane using the first 2 PCs, but apparently using matplotlib to plot over 2mln points is a bad idea. So, I tried again with a sample of 10k rows but after 5 mins still nothing.
```
idx = np.random.randint(10, size=10000)
result = result[idx,:]
plt.scatter(result[:, 0], result[:, 1], c=result[:,result.shape[1]-1]) # 5th column has the labels
```

I'd like to receive some advices on what I'm doing wrong and also how to handle these types of situations in the right way. Also, it's normal that the plot takes so long? I'm using Colab and did some pre-processing (cleaning, standardization, etc..) before PCA.

CodePudding user response：

The results of k-means clustering can be visualized using the principle directions of the observed data. These principle directions are computed using the PCA algorithm. Here is a quick example of doing this with the iris data set:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn import preprocessing
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import itertools

iris = load_iris()

# get flower data
X = iris['data']

# get flower families
labels = iris['target']
nclusters = np.unique(labels).size

# scale flower data
scaler = preprocessing.StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)

# instantiate k-means
seed = 0
km = KMeans(n_clusters=nclusters, random_state=seed)
km.fit(X_scaled)

# predict the cluster for each data point
y_cluster_kmeans = km.predict(X_scaled)

# Compute PCA of data set
pca = PCA(n_components=X.shape[1], random_state=seed)
pca.fit(X_scaled)
X_pca_array = pca.transform(X_scaled)
X_pca = pd.DataFrame(X_pca_array, columns=['PC%i' % (ii   1) for ii in range(X_pca_array.shape[1])]) # PC=principal component

# decide which prediction labels to associate with observed labels
# - search each possible way of transforming observed labels
# - identify approach with maximum agreement
MAX = 0
for ii in itertools.permutations([kk for kk in range(np.unique(y_cluster_kmeans).size)]):

    change = {jj: ii[jj] for jj in range(len(ii))}

    changedPredictions = np.ones(y_cluster_kmeans.size) * -99
    for jj in range(len(ii)):
      changedPredictions[y_cluster_kmeans == jj] = change[jj]

    successful = np.sum(labels == changedPredictions)
    if successful > MAX:
        MAX = successful
        bestChange = change

# transform predictions to match observations
changedPredictions = np.ones(y_cluster_kmeans.size) * -99
for jj in range(len(ii)):
  changedPredictions[y_cluster_kmeans == jj] = bestChange[jj]

# plot clusters for observations and predictions
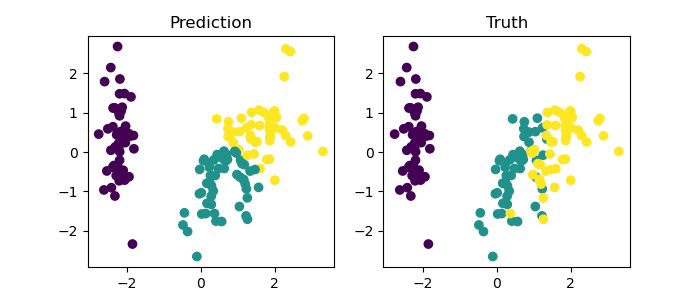
fig, ax = plt.subplots(1, 2, figsize=(7, 3))
ax[0].scatter(X_pca['PC1'], X_pca['PC2'], c=changedPredictions)
ax[1].scatter(X_pca['PC1'], X_pca['PC2'], c=labels)
ax[0].set_title('Prediction')
ax[1].set_title('Truth')

In response to question (1):

It is up to you to choose the number of PCA components, and there are many ways to approach visualizing data in more than 2 dimensions. If I had to plot data with 3 PCA components, I might create animations of scatter plots of the first two components, binning the third component in time.

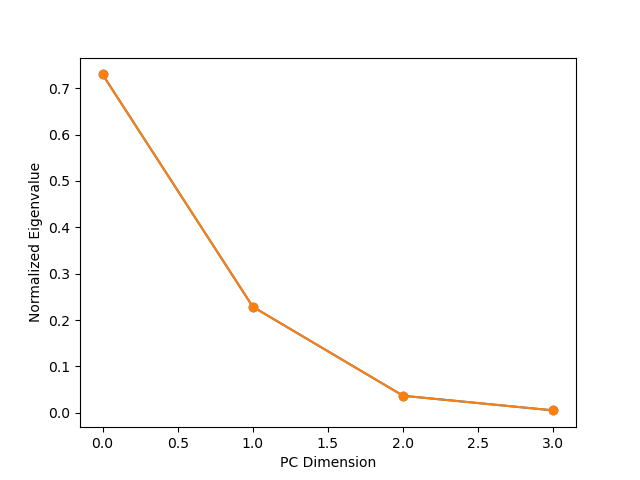
The appropriate number of PCA components can be determined by examining the variation captured by each component (e.g., the eigenvalues), which can be accomplished using pca.explained_variance_:

eigenvalues = pca.explained_variance_
eigenvalues /= eigenvalues.sum()
plt.plot(eigenvalues, marker='o')
plt.xlabel('PC Dimension')
plt.ylabel('Normalized Eigenvalue')

As we can see, about 90% of the variance is captured by the first two PCA components.

So, it is up to you to justify using three PCA components by showing their relative contribution to the total variance. It is typical to only use two, as they often capture most of the variation of the data.

In response to question (2):

Plotting each point takes some time, and that time will add up for millions of points. There is some discussion in this thread about scatter plots with large data sets

If it is hard to intake all of that data when viewing the plot, it might be best to find a numerical/statistical way to assess the k-means clustering. As a simple example, in my Iris data set, I can count the number of failed predictions:

print(r'%.1f percent successful predictions' % (100 * np.sum(labels == changedPredictions) / labels.size))

   83.3 percent successful predictions