I've got the following function:
phi0 = [0; 0]; %initial values
[T,PHI] = ode45(@eqn,[0, 10], phi0,odeset('RelTol',2e-13,'AbsTol',1e-100));
plot(T, PHI(:,1),'-b',T, PHI(:,2),'-g');
title('\it d = 0.1')
w1 = PHI(end,1)/(10000*2*pi) %the limit frequency for phi1
w2 = PHI(end,2)/(10000*2*pi) %the limit frequency for phi2
delta_w = w2 - w1
phi1_at_t_10k = PHI(end,1) %the value phi1(t=10000)
phi2_at_t_10k = PHI(end,2)
function dy_dt = eqn(t,phi)
d = 0.1; %synchronization parameter
n = 3;
g = [ 1.01; 1.02];
f = g-sin(phi/n);
exch = [d;-d]*sin(phi(2)-phi(1));
dy_dt = f exch;
end
The w is calculated by the formula: w_i = (1/2pi)(lim((phi(t)-phi(0))/t) where t->infinity (here it's equal to 10000).
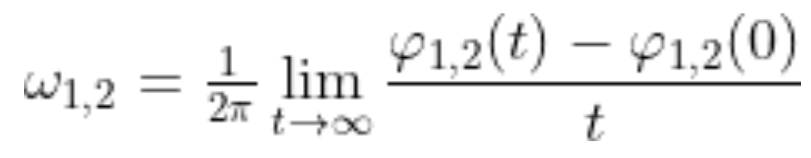
The question is how to plot the dependence of delta_w on different values of d (from d=0 to d=5 with step = 0.1)?
CodePudding user response:
To collect summarize my comments:
First make the parameter d explicit in the ODE function
function dy_dt = eqn(t,phi,d)
n = 3;
g = [ 1.01; 1.02];
f = g-sin(phi/n);
exch = [d;-d]*sin(phi(2)-phi(1));
dy_dt = f exch;
end
Then put the ODE integration and evaluation of the result in its own procedure
function delta_w = f(d)
phi0 = [0; 0]; %initial values
opts = odeset('RelTol',2e-13,'AbsTol',1e-100);
[T,PHI] = ode45(@(t,y)eqn(t,y,d), [0, 10], phi0, opts);
w1 = PHI(end,1)/(10000*2*pi); %the limit frequency for phi1
w2 = PHI(end,2)/(10000*2*pi); %the limit frequency for phi2
delta_w = w2 - w1;
end
And finally evaluate for the list of d values under consideration
d = [0:0.1:5];
delta_w = arrayfun(@(x)f(x),d);
plot(d,delta_w);
This should give a result. If it is not the expected one, further research into assumptions, equations and code is necessary.
