Probability density plots from count/value ("binned") data-CodePudding

I have a data set which contains 27M samples per day. I can reduce this, using count(), to 1500 samples per day, without loss.

When I come to plot, for example, histograms from this, I can use stat="identity" to process the count data considerably faster than the original data.

Is there a similar way to process the count data to obtain ridges using ggridges::geom_density_ridges(), or similar, to get the probability density without having to process the original data set?

CodePudding user response：

It sounds like your current set-up is something like this (obviously with far more cases): a data frame containing a large vector of numeric measurements, with at least one grouping variable to specify different ridge lines.

We will stick to 2000 samples rather than 27M samples for demonstration purposes:

set.seed(1)

df <- data.frame(x = round(c(rnorm(1000, 35, 5), rnorm(1000, 60, 12))),
                 group = rep(c('A', 'B', 'C'), len = 2000))

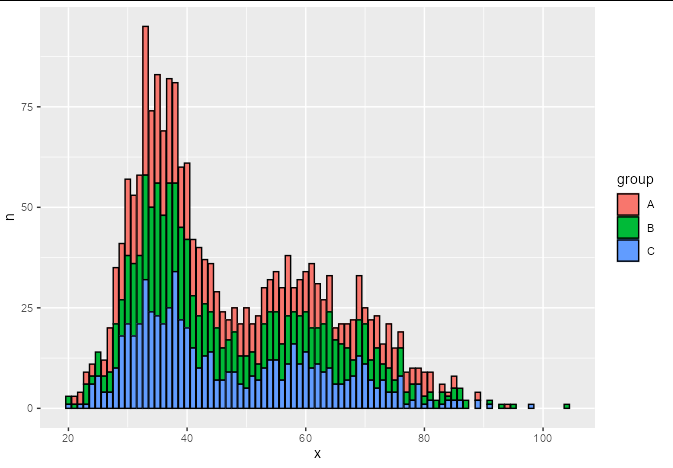
We can reduce these 2000 observations down to ~200 by using count, and plot with geom_histogram using stat = 'identity':

df %>%
  group_by(x, group) %>%
  count() %>%
  ggplot(aes(x, y = n, fill = group))   
  geom_histogram(stat = 'identity', color = 'black')

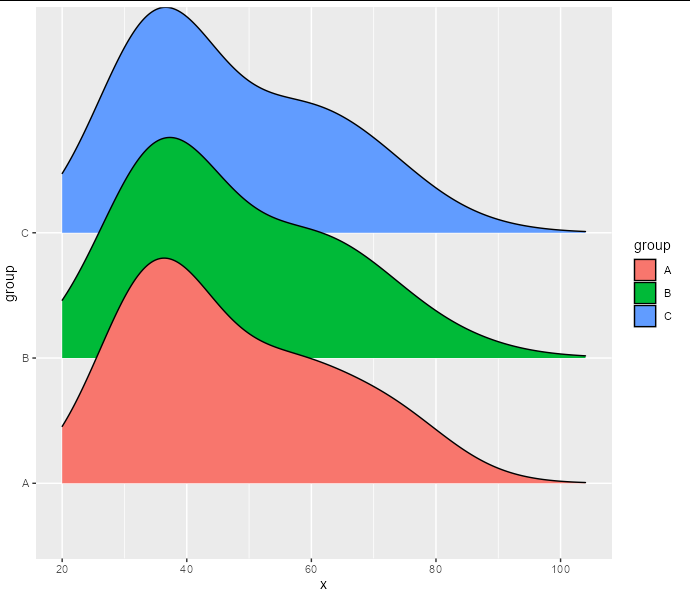
But we want to create density ridgelines from these 200 rows of counts rather than the original data. Of course, we could uncount them and create a density ridgeline normally, but this would be tremendously inefficient. What we can do is use the counts as weights for a density calculation. It seems that geom_density_ridges doesn't take a weight parameter, but stat_density does, and you can tell it to use the density_ridges geom. This allows us to pass our counts as weights for the density calculation.

library(ggridges)

df %>%
  group_by(x, group) %>%
  count() %>%
  ggplot(aes(x, fill = group))  
  stat_density(aes(weight = n, y = group, height = after_stat(density)), 
               geom = 'density_ridges', position = 'identity')

Note that this should give us the same result as creating a ridgleine from our whole data set before counting, since our 'bins' are unique interval values. If your real data is binning continuous data before counting, you will have a slightly less accurate kernel density estimate when using count data, depending on how 'thin' your bins are.