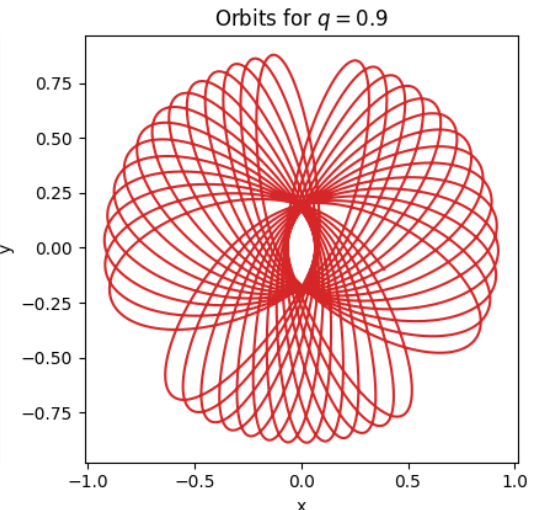
Efficiently calculate sign changes of orbits in an (x, y) phasespace-CodePudding

I have orbits that have been calculated using time integrated. These orbits have coordinates (x, y) for each position. An example of such an orbit can be seen in the image below:

Now using these arrays for x and y, the following series needs to be constructed:

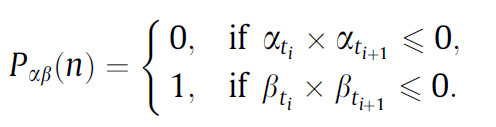
This effectively means, a series where 0 means that x changed signs between time t_n and t_n 1 and 1 means y changed signs between t_n and t_n 1. For the image above, the series would look like: Pxy[n] = 1 0 1 0 1 0 ...

Currently I have found multiple solutions. But they are all pretty slow on the large datasets I use. The array of x and y coordinates for the example orbit shown above has 10,000,000 elements. It needs this many elements since to be accurate enough, the timestep in the integration algorithm needs to be very small. The fastest algorithm I could come up with takes around 5.3 seconds to run. However, this same algorithm needs to be ran 100 times for different orbits. This means it will take a very long time.

I essentially has 2 ways of calculating: The first algorithm is based on this question: "Efficiently detect sign-changes in python" and uses numpy:

def calc_Pxy():
    Pxy = np.full(x.shape, -1)
    Pxy[np.where(np.diff(np.signbit(x)))] = 0
    Pxy[np.where(np.diff(np.signbit(y)))] = 1
    return Pxy[Pxy >= 0]

The second solution just uses a simple for loop:

def calc_Pxy():
    Pxy = []
    for n, [xn, yn] in enumerate(zip(x[:-1], y[:-1])):
        if xn * x[n   1] < 0:
            Pxy.append(0)
        if yn * y[n   1] < 0:
            Pxy.append(1)
    return np.array(Pxy)

!See Edit! After measuring the performance of both methods, it seemed that the first method using numpy is 2.5 times slower than the normal for loop. My first question is, why is that? Is it because it is reshaping arrays which takes time since new arrays need to be created? The second question is, how could I go faster than the for loop?

Finally, another issue with the first numpy method is that when x and y both change signs in the same timestep that in the first example only 1 crossing will be recorded, while in the second one it will in those cases always first put the x and then the y crossing. I prefer that, since you don't lose any data that way.

Any ideas on how to improve the performance would be greatly appreciated.

EDIT: after testing on a large dataset, it seems the numpy method becomes faster if the size of the dataset is increased. My initial tests were based on a small dataset of 20 values, but for 1,000,000 values the numpy way is faster. However I'm still looking for a way to make the behavior of that method the same as the for loop and any further speed improvements are welcome as well off course.

CodePudding user response：

You could simply use numba:

import numba
@numba.njit
def calc_Pxy_numba(x, y):
    Pxy = []
    for n, [xn, yn] in enumerate(zip(x[:-1], y[:-1])):
        if xn * x[n   1] < 0:
            Pxy.append(0)
        if yn * y[n   1] < 0:
            Pxy.append(1)
    return np.array(Pxy)

Note that I avoided using global variables with this approach.

CodePudding user response：

To get better performance, It's better don't use append, you can try this:

import numpy as np
import numba as nb

x = np.random.uniform(-2, 2, 10_000_000)
y = np.random.uniform(-2, 2, 10_000_000)

@nb.njit('float32[:](float64[:], float64[:])')
def calc_Pxy5(x, y):
    Pxy = np.empty(len(x) len(y), dtype=np.float32)
    idx = 0
    for xn, yn in zip(x[:-1] * x[1:] , y[:-1] * y[1:]):
        if xn < 0:
            Pxy[idx] = 0
            idx  = 1
        if yn < 0:
            Pxy[idx] = 1
            idx  = 1
    return Pxy[:idx]


@nb.njit('float32[:](float64[:], float64[:])')
def calc_Pxy6(x, y):
    Pxy = np.empty(len(x) len(y), dtype=np.float32)
    idx = 0
    for xn, yn in zip(np.diff(np.signbit(x)) , np.diff(np.signbit(y))):
        if xn :
            Pxy[idx] = 0
            idx  = 1
        if yn :
            Pxy[idx] = 1
            idx  = 1
    return Pxy[:idx]

benchmark on colab:

>>> %timeit calc_Pxy5(x,y)
10 loops, best of 5: 176.1 ms per loop

>>> %timeit calc_Pxy6(x,y)
10 loops, best of 5: 178 ms per loop

>>> np.all(calc_Pxy5(x,y) == calc_Pxy6(x,y))
True

CodePudding user response：

Combining the ideas of methods 1 and 2:

def calc_Pxy3():
    Pxy = []
    for [xn, yn] in zip(np.diff(np.signbit(x)), np.diff(np.signbit(y))):
        if xn:
            Pxy.append(0)
        if yn:
            Pxy.append(1)
    return np.array(Pxy)

we get a speedup of about 5 times compared to method 2 (but still 5 times slower then method 1).

Results for n = 10_000_000 random x/y values:

%timeit calc_Pxy1()  # numpy
253 ms ± 3.08 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

%timeit calc_Pxy2()  # simple loop
10.8 s ± 124 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

%timeit calc_Pxy3()
2.18 s ± 17.2 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Update:

def calc_Pxy4():
    z = np.ravel((np.where(np.diff(np.signbit(x)), 0, -1), np.where(np.diff(np.signbit(y)), 1, -1)), order='F')
    return np.compress(z >= 0, z)

with

%timeit calc_Pxy4()
361 ms ± 5.27 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

is faster than Dominik Stańczak's straightforward numba solution (422 ms) but slower than I'mahdi's optimized numba solution (175 ms).