Least Squares Regression for Probability Density function but I get incorrect dimensions error-CodePudding

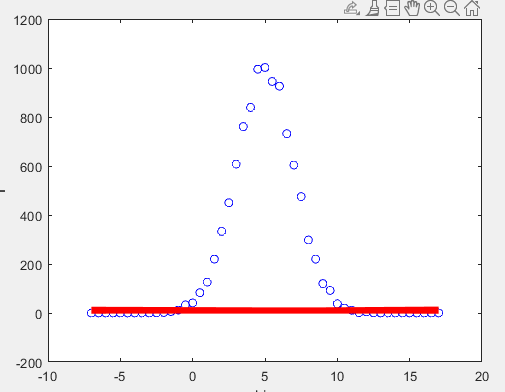
I'm trying to perform least-squares regression to this probability density function but I get prompted to perform .* operation in matlab instead of the standard * operation in evaluating Astar. When I do this, I get weird flat lines on the bottom part of my plot.

The code:

N = 10000;
mu = 5; sigma = 2;
r = randn(N,1);
x = mu sigma*r;
bin=mu-6*sigma:0.5:mu 6*sigma;
f=hist(x,bin);
plot(bin,f,'bo'); hold on;
xlabel('bin');
ylabel('f');

y_ = f;
x_ = bin;


H = [ones(length(y_),1),x_'];
Astar = inv(H'*H)*H'.*y_;        % Line in Question
% Astar = inv(H'*H)*H'*y_;       % Initial form, but Matlab prompts to perform .* instead
Ytilde = H*Astar;
plot(x_,Ytilde, 'r-','LineWidth',1)

Resulting Plot:

What could be the reason?

CodePudding user response：

For better or for worse, some of MATLAB's commands return row vectors, and some return column vectors. Often (or perhaps almost always) statistics is done with vectors of observations being column vectors. As far as I know, this is just something one has to be careful of when using certain commands.

Your issue comes from the fact that y_ is a row vector, whereas normal statistic formulas suppose it is a column vector. In the 'line in question', if you use *y_' instead of .*y_ (i.e. Astar = inv(H'*H)*H'*y_';) that gives you the expected behaviour.

The colon operator in MATLAB generates a row vector, and hist does the same thing. These are the root of the problem. These can be resolved in a few ways.

One way would be to transpose them when they are produced in the first part of your code. Another way would be to transpose them when you instantiate x_ and y_ (done below). Another way (and probably the worst way) would be to leave them as row vectors and transpose them each time you use them. Overall the solution would depend on the rest of your code, and it would be best to keep it consistent.

===

N = 10000;
mu = 5; sigma = 2;
r = randn(N,1);
x = mu sigma*r;
bin=mu-6*sigma:0.5:mu 6*sigma;
f=hist(x,bin);
figure;
scatter(bin,f); hold on;
xlabel('bin');
ylabel('f');

y_ = f';
x_ = bin';


H = [ones(length(y_),1),x_];
Astar = inv(H'*H)*H'*y_;        % Line in Question
Ytilde = H*Astar;
plot(x_,Ytilde, 'r-','LineWidth',1)

===

[Also note that you still get a horizontal line, but y ~= 200. This is expected given the curve is symmetric, and this also agrees with MATLAB's inbuilt polyfit and polyval functions.]

[Also note that hist is no longer recommended.]