Creating image of a two-variable function and finding its optimum in R-CodePudding

I am doing some tasks for my degree and stuck upon a problem of imaging a multivariable function. Following:

fb<-function(x) {5*x[1]^2 2*x[1]*x[2] 4*x[2]^2 4*x[1]-2*x[2]-2}
> x<--50:50
> y<--50:50
> z<-outer(x,y,fb)
Error in FUN(X, Y, ...) : unused argument (Y)

More than that, I need to find an optimum with maximum on point, but it gives out next when I try without vectors:

 optim(c(0,0), fb, control=list(fnscale=-5))
Error in fn(par, ...) : argument "y" is missing, with no default

Please advice.

CodePudding user response：

It looks as though you have a function of two variables, x[1] and x[2], that you are passing into your function as a single vector, x. This will cause problems with vectorization of the output. A better way to write it would be

fb <- function(x, y) {
  5 * x^2   2*x * y   4 * y^2   4 * x - 2 * y - 2
}

This allows you to visualize the function as a surface, for example using persp:

x <- -50:50
y <- -50:50
z <- outer(x, y, fb)

persp(x, y, z)

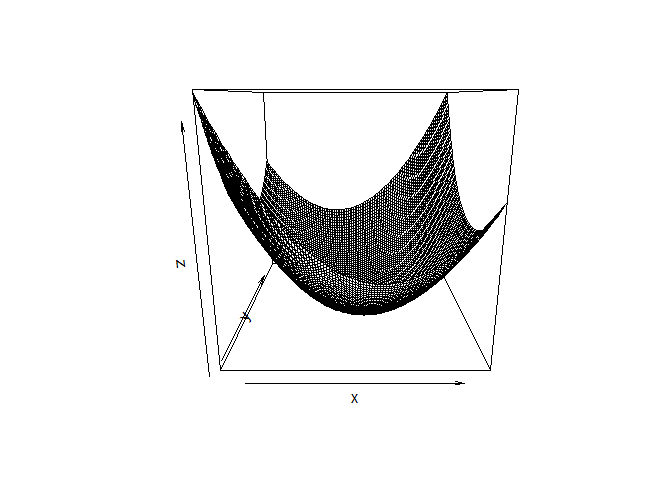
To get this working with optim, create a wrapper function that puts x and y into a single vector so that it is functionally equivalent to your original function:

result <- optim(c(0, 0), function(x) fb(x[1], x[2]))$par
result
#> [1] -0.4736532  0.3684892

To show this is the correct result, we will plot the optimum point on a 2D representation of the surface.

library(ggplot2)

ggplot(cbind(expand.grid(x = x, y = y), z = c(z)), aes(x, y, fill = z))  
  geom_raster()  
  scale_fill_viridis_c()  
  geom_point(x = result[1], y = result[2], color = "white")

^{Created on 2022-06-15 by the reprex package (v2.0.1)}

CodePudding user response：

If you want to use outer, you should try it with Vectorize

x <- -50:50
y <- -50:50
z <- outer(x, y, Vectorize(function(a, b) fb(c(a, b))))

and for optiom

> optim(c(0, 0), fb, lower = c(-50, -50), upper = c(50, 50), method = "L-BFGS-B")
$par
[1] -0.4736842  0.3684211

$value
[1] -3.315789

$counts
function gradient
       7        7

$convergence
[1] 0

$message
[1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"