How to solve a cubic function with more than hundred pairs of known dependent and independent variab-CodePudding

I try to find out how to solve a cubic function with independent variable (x) and dependent variable f(x) known but coefficient a, b, c and constant d unknown. I tried sympy but realized it only works for 4 pairs. Now I try to explore some possibilities to solve this (by finding the actual value for coefficient a/b/c and constant d). Any advice are greatly appreciated.

Below is the code which obviously does not work and returned an empty list because there are more than hundred of pairs.

from sympy import Eq, solve
from sympy.abc import a,b,c,d, x

formula = a*x**3   b*x**2   c*x   d  # general cubic formula

xs = [28.0, 29.0, 12.0, 12.0, 42.0, 35.0, 28.0, 30.0, 32.0, 46.0, 18.0, 28.0, 28.0, 64.0, 
38.0, 18.0, 49.0, 37.0, 25.0, 24.0, 42.0, 50.0, 12.0, 64.0, 23.0, 35.0, 22.0, 16.0, 44.0, 
77.0, 26.0, 44.0, 38.0, 37.0, 45.0, 42.0, 24.0, 42.0, 12.0, 46.0, 12.0, 26.0, 37.0, 15.0, 
67.0, 36.0, 43.0, 36.0, 45.0, 82.0,
44.0, 30.0, 33.0, 51.0, 50.0]

fxs = [59.5833333333333, 59.5833333333333, 10.0, 10.0, 47.0833333333333, 51.2499999999999, 
34.5833333333333, 88.75, 63.7499999999999, 34.5833333333333, 51.2499999999999, 10.0, 
63.7499999999999, 51.0, 59.5833333333333,47.0833333333333, 49.5625, 43.5624999999999, 
63.7499999999999, 10.0, 76.25, 47.0833333333333,10.0, 51.2499999999999,47.0833333333333,10.0, 
35.0, 51.2499999999999, 76.25, 100.0, 51.2499999999999, 59.5833333333333, 63.7499999999999, 
76.25, 100.0, 51.2499999999999, 10.0, 22.5, 10.0, 88.75, 10.0, 59.5833333333333, 
47.0833333333333, 34.5833333333333, 51.2499999999999, 63.7499999999999,63.7499999999999, 10.0, 
76.25, 62.1249999999999, 47.0833333333333, 10.0, 76.25, 47.0833333333333, 88.75]

sol = solve([Eq(formula.subs(x, xi), fx) for xi, fx in zip(xs, fxs)])
print(sol)  
[]

CodePudding user response：

For curve-fitting, I recommend using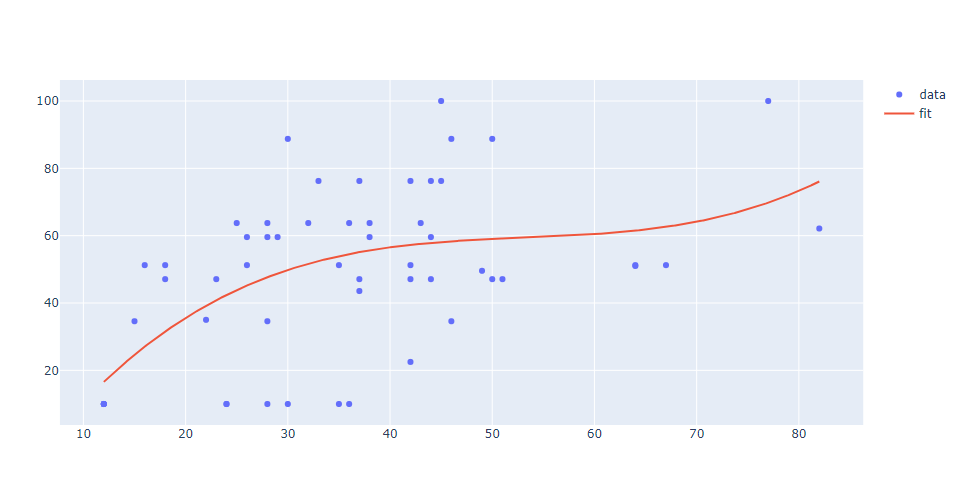

CodePudding user response：

How you might approach this with SymPy (assuming you want a least squared error solution):

In [2]: errors_squared = [(fx - formula.subs(x, xi))**2 for fx, xi in zip(xs, fxs)]

In [3]: error = Add(*errors_squared)

In [4]: sympy.linsolve([error.diff(v) for v in [a, b, c, d]], [a, b, c, d])
Out[4]: {(0.00019197277106452, -0.0310483217324413, 1.68127292155383, 7.51784205803798)}