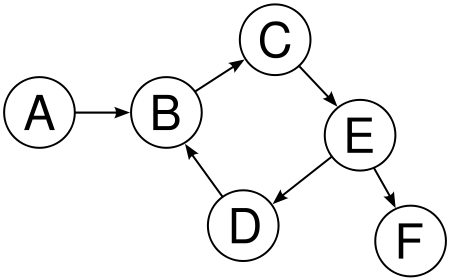
My question is about infecting an entire graph with the smallest set of vertices that will be deemed as infected. The question goes something like this. For a vertex A in a (not necessarily simple) directed graph, A will become infected if for all in-edges of the form (A, B) (it's a directed graph so A will be pointing towards B) B is also infected. If we were to take a specific example:

In this case, if the vertices E, A were infected:

Iteration 1:

vertices F, D are infected because of the fact that the only vertex that points to them is E and E is infected.

Iteration 2:

The vertex B is infected as both vertices A and D are infected.

Iteration 3:

Finally the vertex C is infected as a result of the infection of vertex B from Iteration 2.

In this case, the infected set {E, A} that I chose was able to infect the entire graph. Obviously, this isn't always possible as in the case with the infected set of {B} (the vertex A doesn't end up infected as B doesn't point to it and thus there is no way of reaching it) or the infected set of {A} (the vertex B is not infected as it has a perfectly healthy parent in D).

I really want to find an algorithm that finds the smallest set of infected vertices that will end up infecting the entire graph after an arbitrary number of iterations. Does something like this already exist? If so which algorithm would I use? Any help is greatly appreciated. Thanks in advance! :)

Edit: Just for clarification, for vertices that are a self-loop, it would necessarily have to be in the infected set as that's the only way that it can get infected.

CodePudding user response：

The difficulty is that all source nodes for each node must be infected to infect a node. So, thre real.ity is that every edge must carry infection. So -

- LOOP over the roots ( nodes with only out edges )
    Add root to solution
    Mark all edges reachable from root
    If every edge marked
         STOP
 - LOOP over every node that has unmarked out edges
       Add node to solution
       Mark all edges reachable from node
       If every edge marked
             STOP
 - LOOP over disconnected nodes
       Add node to solution
 STOP

Note that this does not always give the optimal solution. It gives a successful solution that infects every node. Brute force optimization: place algorithm in loop over enumeration of node orders and keep the solution if it is improved.

CodePudding user response：

This problem is NP-hard.

The vertices which are part of this minimal infection set fall into two buckets. The first bucket is all nodes with no incoming edges. The second bucket is a minimal set of nodes that makes the graph acyclic. (If you left a cycle, then things in that cycle don't get infected. Conversely if you leave no cycles, then it is easy to prove by induction that the whole graph winds up infected.)

Very importantly, if you were able to solve this problem, then it would be easy to take the solution, remove from it the nodes which had no incoming edges, and then you're left with the minimal feedback vertex set. This would give an algorithm to solve an NP-hard problem for arbitrary graphs.

(Yes, yes, I know that the Wikipedia article says NP-complete everywhere. It is wrong. The question, "Is there a feedback vertex set of size k" is NP-complete. The question, "What is the smallest feedback vertex set" is NP-hard because, given a claimed minimal set, you don't have a polynomial algorithm to verify that no minimal set is shorter. That is, the decision problem is NP-complete and the optimization problem is NP-hard.)