Different predictions on every run with GaussianProcessRegressor-CodePudding

I'm trying to predict and find a maximum of a target function using Gaussian Processes. However, at times, the predictions I get from the GPR are flat and constant throughout the range. If I run it again, it may work fine. I'm attaching here some code to reproduce:

import matplotlib.pyplot as plt
import numpy as np
from sklearn.gaussian_process.kernels import Matern
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.preprocessing import StandardScaler

use_scalar = False

scalerx = StandardScaler()
scalery = StandardScaler()

data_target = np.array([[ 4.11527487e 00, -5.25998354e-02],
                       [ 9.87746489e-02, -4.13503230e-02],
                       [ 3.57381547e 00, -5.25998354e-02],
                       [ 1.60683672e 00, -5.25998354e-02],
                       [ 5.26929603e 00, -6.18080378e-02],
                       [ 9.08232311e-01, -5.25998354e-02],
                       [ 2.39112060e-01, -3.52116406e-02],
                       [ 4.29874823e 00, -4.23911691e-02],
                       [ 9.88334539e-01, -5.25998354e-02],
                       [ 3.10196661e 00, -5.25998354e-02],
                       [ 7.87734943e-01, -5.25998354e-02],
                       [ 8.27486483e-01, -5.16990900e-02],
                       [ 3.80523113e 00, -5.25998354e-02],
                       [ 7.03828442e-01, -2.22452462e-02],
                       [ 5.83227361e 00, -3.09045196e-02],
                       [ 4.65850859e 00, -2.24894464e-02],
                       [ 5.35498380e 00, -4.55683947e-02],
                       [ 5.15052521e 00, -2.59802818e-02],
                       [ 3.43894560e 00, -5.25998354e-02],
                       [ 3.40215825e 00, -5.25998354e-02],
                       [ 0.00000000e 00, -4.35041189e-03],  # <- manually added point
                       [ 6.28318531e 00, -4.35041189e-03]]) # <- manually added point

krnl = Matern(nu=2.5)
gp = GaussianProcessRegressor(kernel=krnl, alpha=1e-6, normalize_y=True, n_restarts_optimizer=5, random_state=np.random.RandomState())

if(use_scalar):
    # gp.set_params(kernel__length_scale=0.)
    scalerx.fit(data_target[:,0:1])
    scalery.fit(data_target[:,1:])
    X = scalerx.transform(optimizer._space.params)
    Y = scalery.transform(optimizer._space.target)
else:
    X = data_target[:,0:1]
    Y = data_target[:,1:]

gp.fit(X, Y)

# predict
x_pnts = np.linspace(0, 6.28, 1000).reshape(-1,1)
if(use_scalar):
    x = scalerx.transform(x_pnts)
else:
    x = x_pnts

mu, sigma = gp.predict(x, return_std=True)
if(use_scalar):
    mu = scalery.inverse_transform(mu.reshape(-1,1))

plt.scatter(data_target[:,0], data_target[:,1], marker='*')
plt.scatter(x_pnts, mu, marker='.')

plt.show()

I tried scaling, I tried setting the length_scale but neither really helped (unless I'm doing it wrong). How is it possible that I'm getting different predictions for the same data? How do I correct this behavior?

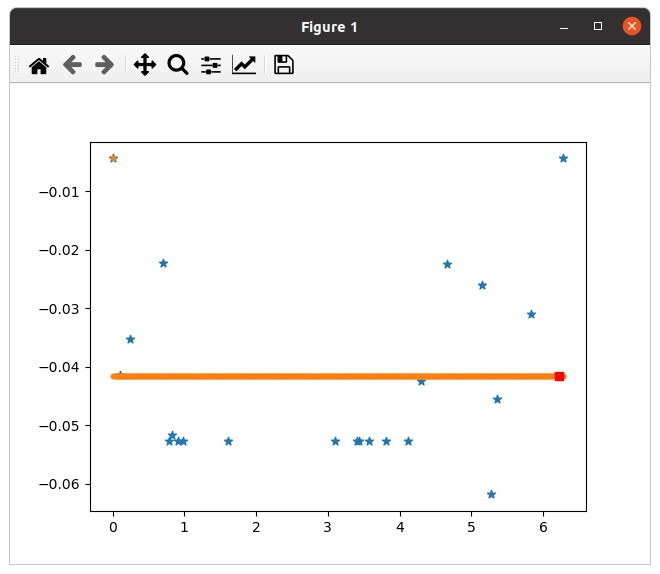
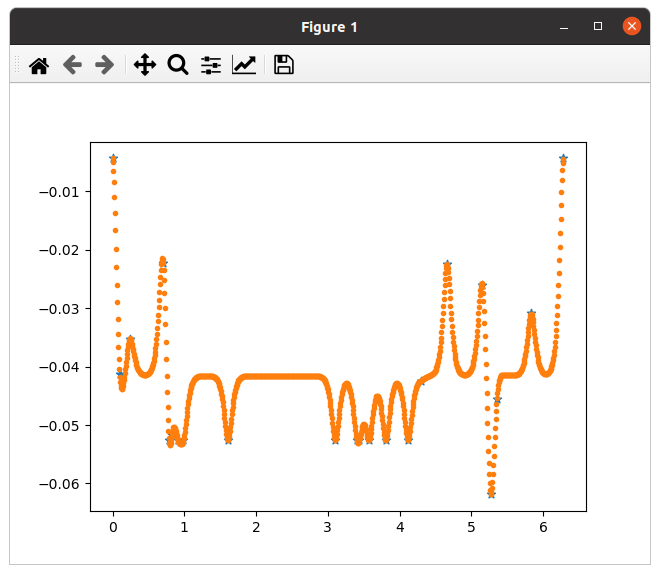
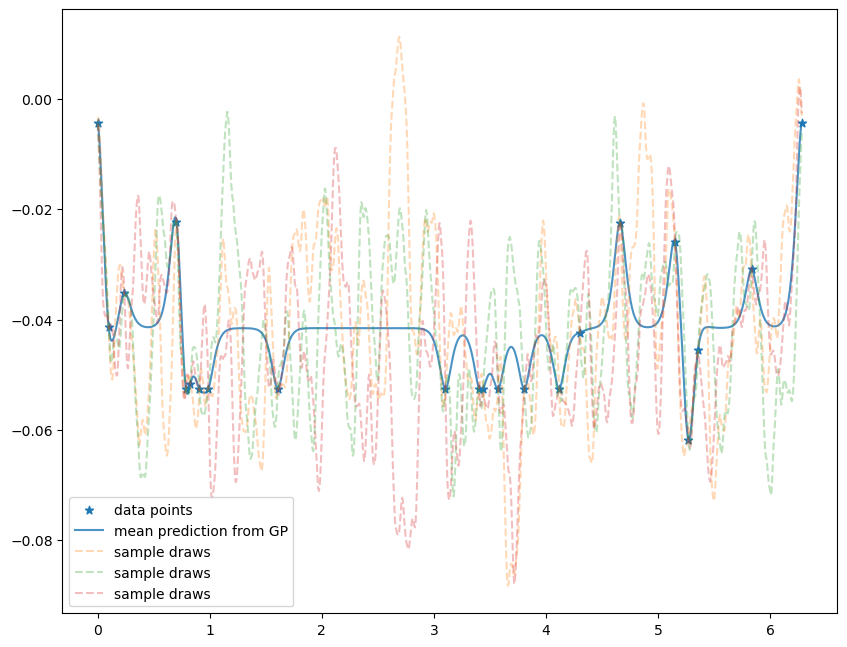
and there's also a different behavior that is mostly flat but predicts just the points that are trained with.

CodePudding user response：

Well, you're explicitly putting in randomness via random_state=np.random.RandomState(), and then you're not seeding it anywhere, so of course it's going to be different every run. Try random_state=np.random.RandomState(1337).

I've adapted your code a little, using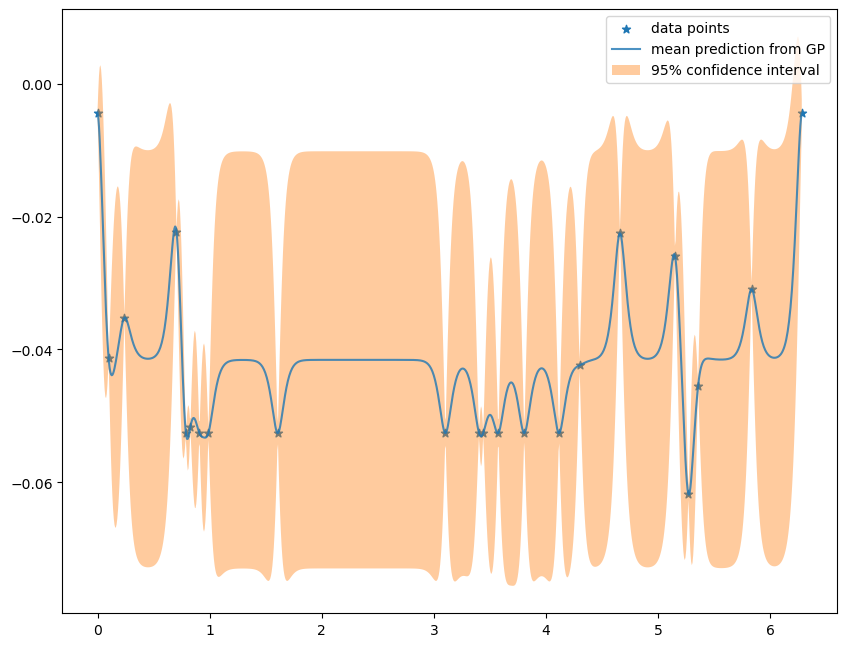

As you can see, the fit is not that great (my implementation probably leaves something to be desired... not sure what, though). However, the important point I wanted to illustrate here is seen if we turn on the commented-out line at the end, and switch of the confidence interval:

Here you can see a few samples of the inherently random predictions you were getting before. Taking their standard deviation (can be done analytically AFAIK, which is neat) gives you the orange confidence interval from the plot before.