Error in nls, step factor reduced below minFactor-CodePudding

I have the following dataframe:

> dput(df_acf)
structure(list(x = c(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10), y = c(1, 
0.0595936565187637, 0.0376022880804335, 0.0521100393333187, 0.0720561234389795, 
0.0262258507877819, -0.0126644770510529, 0.18604968147151, 0.115018192163521, 
-0.0476175556946567, -0.183213245514104)), class = "data.frame", row.names = c(NA, 
-11L))

which I would like to fit using this non linear function

f <- function(t, coeff_sigma, coeff_alpha,coeff_omega) {
  coeff_sigma * exp(-coeff_alpha*t)*cos(coeff_omega*t)
}

However, when using nls

fit <- nls(y~f(x,coeff_sigma,coeff_alpha,coeff_omega), data=df_acf, start=list(coeff_sigma=0.8, coeff_alpha=0.62, coeff_omega=0.65),control = nls.control(maxiter = 1000))

I get this error: error in nls, step factor reduced below minFactor

CodePudding user response：

If you are open to other parametric models then this easily fits:

fo <- y ~ a * (1   b * x) ^ -c
fit2 <- nls(fo, df_acf, start = list(a = 1, b = 1, c = 1))

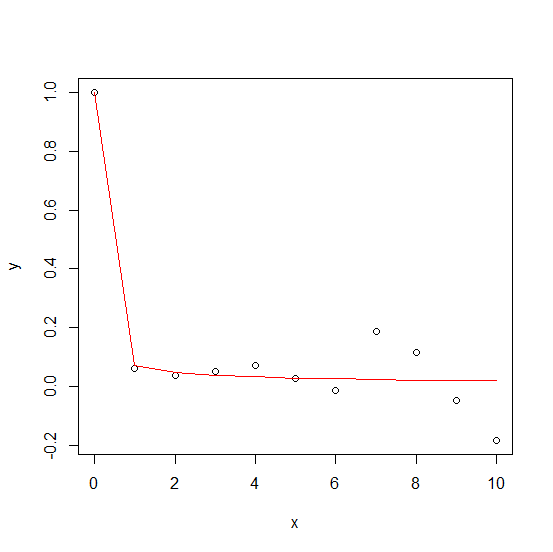
plot(df_acf)
lines(fitted(fit2) ~ x, df_acf, col = "red")

giving:

CodePudding user response：

Using nls2 seems to work for me at least with the brute-force algorithm.

library(nls2)
nls2(y~f(x,coeff_sigma,coeff_alpha,coeff_omega), data=df_acf, start=list(coeff_sigma=0.8, coeff_alpha=0.62, coeff_omega=0.65),control = nls.control(maxiter = 1000), algorithm = "brute-force")
Nonlinear regression model
  model: y ~ f(x, coeff_sigma, coeff_alpha, coeff_omega)
   data: NULL
coeff_sigma coeff_alpha coeff_omega 
       0.80        0.62        0.65 
 residual sum-of-squares: 0.2355

Number of iterations to convergence: 1 
Achieved convergence tolerance: NA