What is the Big Oh, Big Omega and Big Theta of this algorithm?-CodePudding

I am reading The algorithm design manual and i am stucked at this question

Growth of Functions and Aymptotic Notation

When we study algorithms, we are interested in characterizing them according to their efficiency.
We are usually interesting in the order of growth of the running time of an algorithm, not in the exact running time. This is also referred to as the asymptotic running time.
We need to develop a way to talk about rate of growth of functions so that we can compare algorithms.
Asymptotic notation gives us a method for classifying functions according to their rate of growth.

1. Big-O Notation

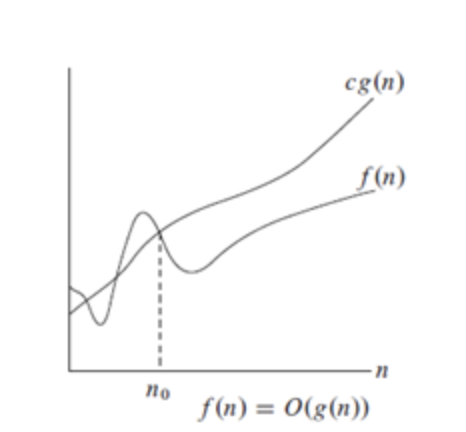
Definition: f (n) = O(g(n)) iff there are two positive constants c and n0 such that
```
       f (n)| ≤ c |g(n)| for all n ≥ n0
```
If f (n) is nonnegative, we can simplify the last condition to
```
        0 ≤ f (n) ≤ c g(n) for all n ≥ n0
```
We say that

f(n) is big-O of g(n)

As n increases, f (n) grows no faster than g(n). In other words, g(n) is an asymptotic upper bound on f (n).

2. Ω notation

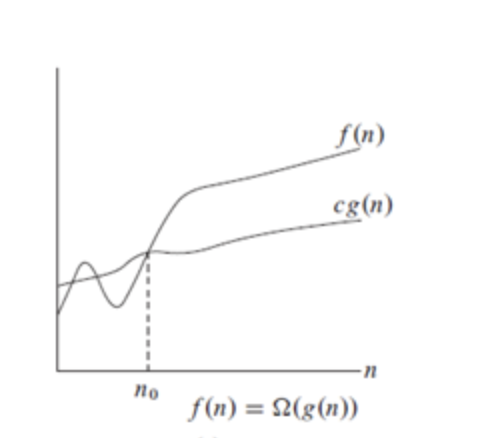
Definition: f (n) = Ω(g(n)) iff there are two positive constants c and n0 such that
```
     f (n)| ≥ c |g(n)| for all n ≥ n0
```
If f (n) is nonnegative, we can simplify the last condition to
```
     0 ≤ c g(n) ≤ f (n) for all n ≥ n0
```
We say that

f (n) is omega of g(n)

As n increases, f(n) grows no slower than g(n). In other words, g(n) is an asymptotic lower bound on f(n).

3. Θ notation

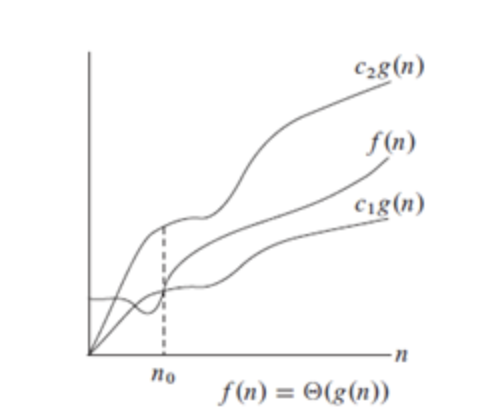
Definition: f (n) = Θ(g(n)) iff there are three positive constants c1, c2 and n0 such that
```
          c1|g(n)| ≤ |f (n)| ≤ c2|g(n)| for all n ≥ n0
```

If f(n) is nonnegative, we can simplify the last condition to

          0 ≤ c1 g(n) ≤ f (n) ≤ c2 g(n) for all n ≥ n0

As n increases, f(n) grows at the same rate as g(n). In other words, g(n) is an asymptotically tight bound on f(n).