How to automate plotting 3 different regular polygons recursively?-CodePudding

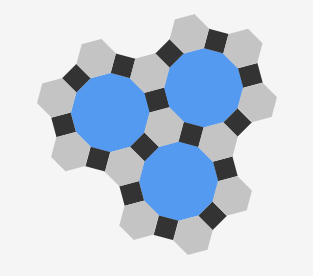
I want to plot 3 regular polygons - squares (4 sides), hexagons (6 sides) and dodecagons (12 sides) in a way that it produces a similar plot to the following figure:

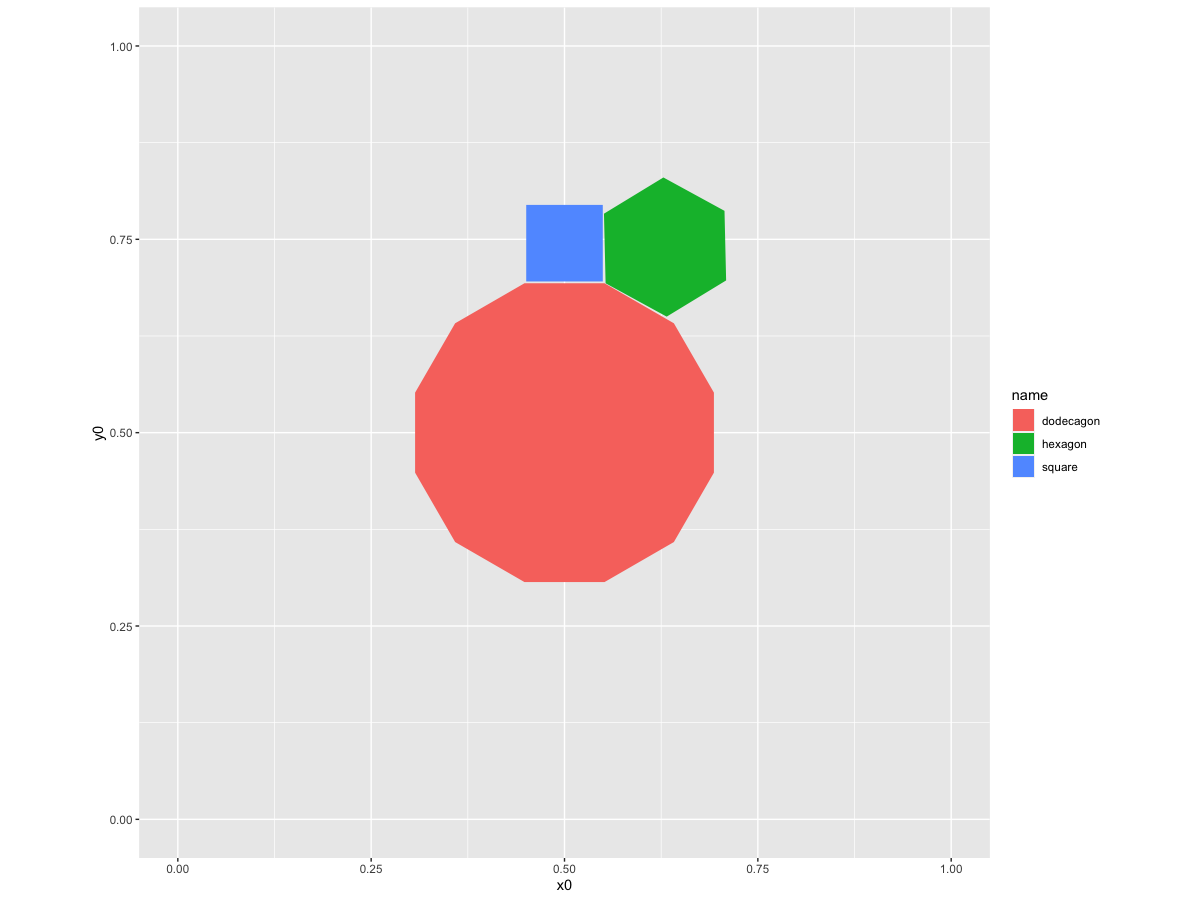
So far, I have been hardcoding with the ggforce package to achieve my goal:

library(ggplot2)
library(ggforce)

df = data.frame(name = c("dodecagon", "square", "hexagon"),
                x0 = c(0.5, 0.5, 0.63),
                y0 = c(0.5, 0.745, 0.74),
                sides = c(12, 4, 6),
                angle = c(0, 0, -0.5),
                r = c(0.2, 0.07, 0.09))

ggplot(data = df)  
        geom_regon(aes(x0 = x0, y0 = y0, sides = sides, angle = angle, r = r, fill = name))  
        coord_fixed(xlim = c(0, 1), ylim = c(0, 1))

which produces:

As you can see, the polygons are not nicely aligned and it would take unreasonably long to actually achieve what I want to achieve.

Essentially, I would like to have a function which takes the number of dodecagons (12 sided polygon) as its argument and plots squares (4 sided polygon) and hexagons (6 sided polygon) around the dodecagon(s).

P.S. it does not have to be done using ggforce, but I would prefer to eventually have a ggplot2 plot.

CodePudding user response：

I'm not sure what the easy way is to do this, but let me show you the hard way. First, define a function that produces a data frame of the co-ordinates of a regular dodecagon, given its centre co-ordinates and its radius (i.e. the radius of the circle on which its vertices sit):

dodecagon <- function(x = 0, y = 0, r = 1) {
  theta <- seq(pi/12, 24 * pi/12, pi/6)
  data.frame(x = x   r * cos(theta), y = y   r * sin(theta))
}

Now define functions which take the co-ordinates of a line segment and return a data frame of x, y co-ordinates representing a square and a hexagon:

square <- function(x1, x2, y1, y2) {
  theta <- atan2(y2 - y1, x2 - x1)   pi/2
  r <- sqrt((x2 - x1)^2   (y2 - y1)^2)
  data.frame(x = c(x1, x2, x2   r * cos(theta), x1   r * cos(theta), x1),
             y = c(y1, y2, y2   r * sin(theta), y1   r * sin(theta), y1))
}

hexagon <- function(x1, x2, y1, y2) {
  theta <- atan2(y2 - y1, x2 - x1)
  r <- sqrt((x2 - x1)^2   (y2 - y1)^2)
  data.frame(x = c(x1, x2, x2   r * cos(theta   pi / 3),
                   x2   r * cos(theta   pi / 3)   r * cos(theta   2 * pi / 3),
                   x1   r * cos(theta   2 * pi / 3)   r * cos(theta   pi / 3),
                   x1   r * cos(theta   2 * pi / 3), 
                   x1),
           y = c(y1, y2, y2   r * sin(theta   pi / 3),
                   y2   r * sin(theta   pi / 3)   r * sin(theta   2 * pi / 3),
                   y1   r * sin(theta   2 * pi / 3)   r * sin(theta   pi / 3),
                   y1   r * sin(theta   2 * pi / 3), 
                   y1))
}

Finally, write a function that co-ordinates the first 3 to return a single data frame of all the co-ordinates, labelled by shape type and with a unique number for each polygon:

pattern <- function(x = 0, y = 0, r = 1) {
  d <- cbind(dodecagon(x, y, r), shape = "dodecagon", part = 0)
  squares <- lapply(list(1:2, 3:4, 5:6, 7:8, 9:10, 11:12),
                    function(i) {
                    cbind(
                      square(d$x[i[2]], d$x[i[1]], d$y[i[2]], d$y[i[1]]),
                      shape = "square", part = i[2]/2)
                    })
  hexagons <- lapply(list(2:3, 4:5, 6:7, 8:9, 10:11, c(12, 1)),
                     function(i) {
                     cbind(
                      hexagon(d$x[i[2]], d$x[i[1]], d$y[i[2]], d$y[i[1]]),
                      shape = "hexagon", part = i[1]/2   6)
                    })
  rbind(d, do.call(rbind, squares), do.call(rbind, hexagons))
}

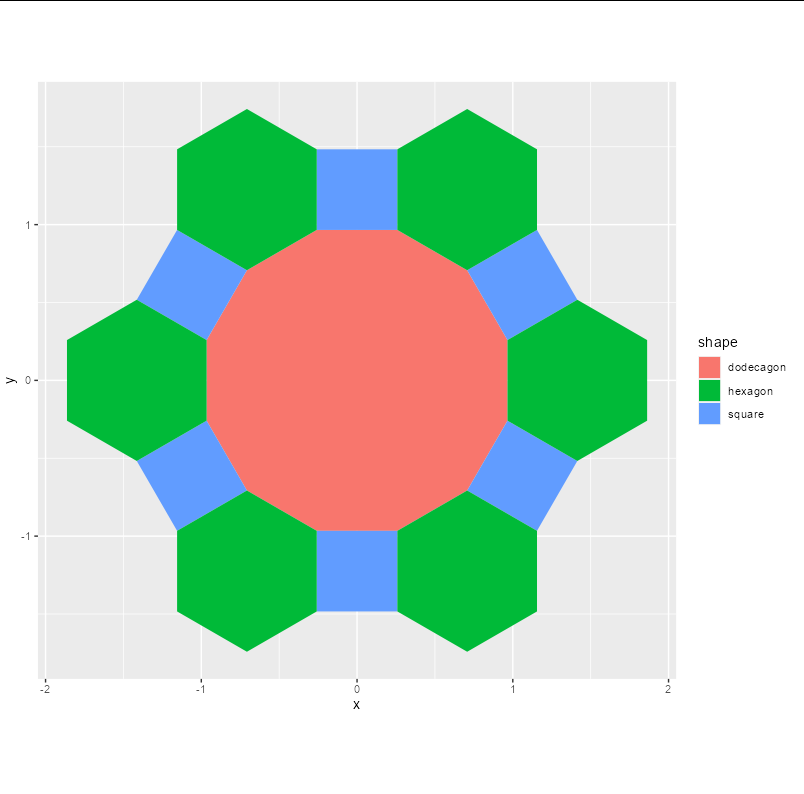
All that done, plotting is trivial:

library(ggplot2)

ggplot(data = pattern(), aes(x, y, fill = shape, group = part))   
  geom_polygon()  
  coord_equal()

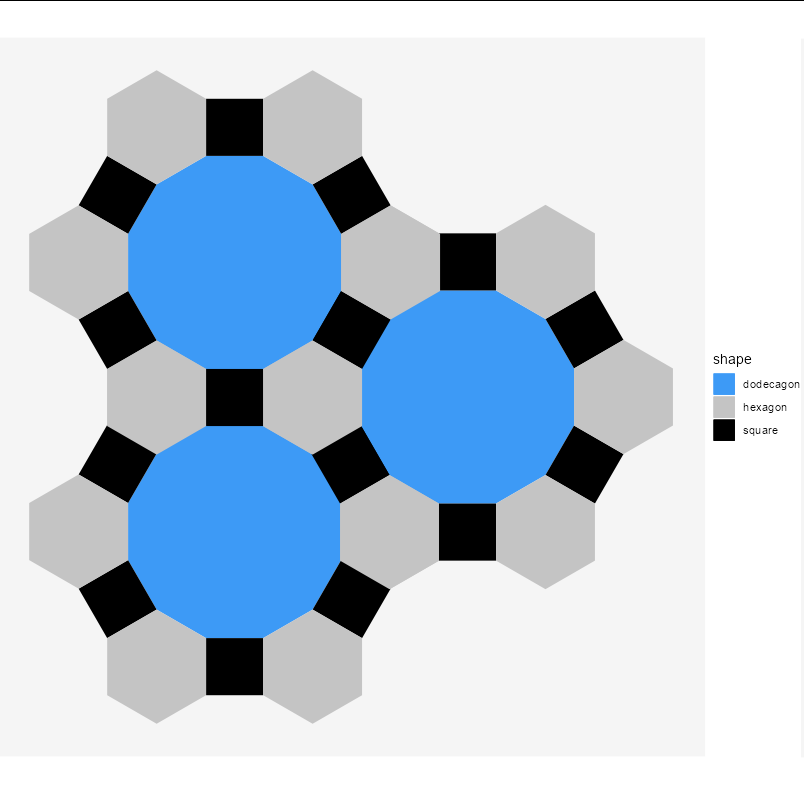
Or, reproducing your original figure:

ggplot(data = pattern(), aes(x, y, fill = shape, group = part))   
  geom_polygon()  
  geom_polygon(data = pattern(2.111, 1.22))  
  geom_polygon(data = pattern(0, 2.44))  
  scale_fill_manual(values = c("#3d9af6", "#c4c4c4", "black"))  
  coord_equal()  
  theme_void()  
  theme(panel.background = element_rect(fill = "#f5f5f5", color = NA))