When does order of alternation matter in antlr?-CodePudding

In the following example, the order matters in terms of precedence:

grammar Precedence;
root: expr EOF;

expr
    : expr (' '|'-') expr
    | expr ('*' | '/') expr
    | Atom
    ;

Atom: [0-9] ;
WHITESPACE: [ \t\r\n] -> skip;

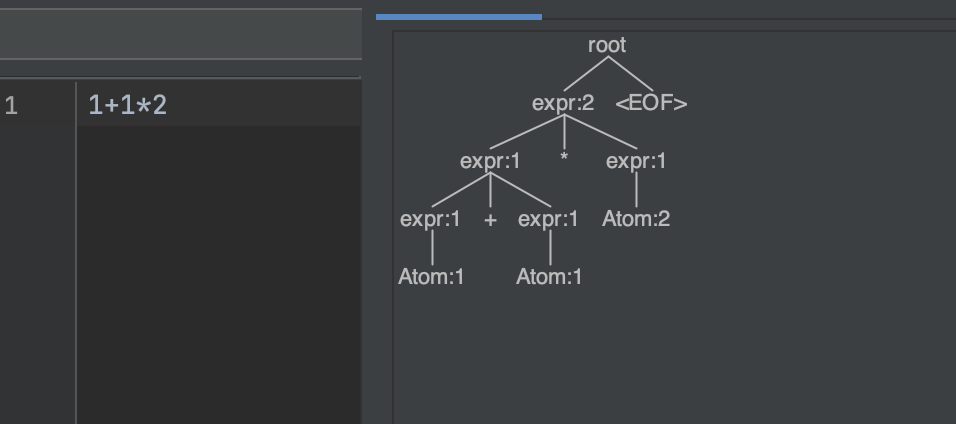
For example, on the expression 1 1*2 the above would produce the following parse tree which would evaluate to (1 1)*2=4:

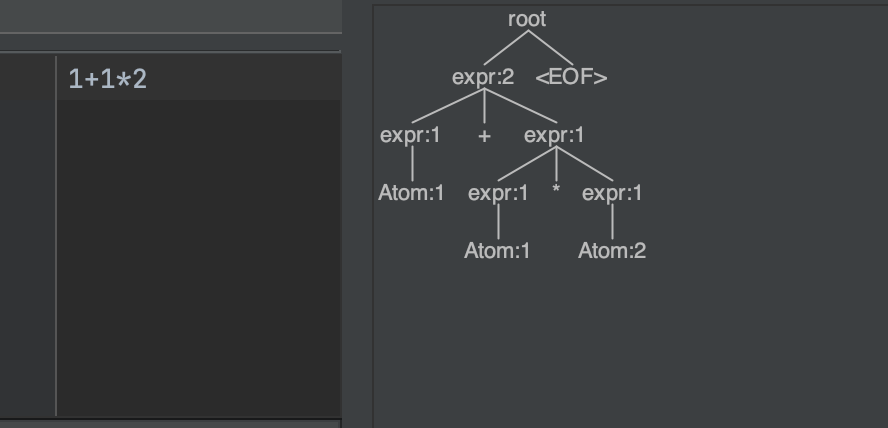
Whereas if I changed the first and second alternations in the expr I would then get the following parse tree which would evaluate to 1 (1*2)=3:

What are the 'rules' then for when it actually matters where the ordering in an alternation occurs? Is this only relevant if it one of the 'edges' of the alternation recursively calls the expr? For example, something like ~ expr or expr expr would matter, but something like func_call '(' expr ')' or Atom would not. Or, when is it important to order things for precedence?

CodePudding user response：

If ANTLR did not have the rule to give precedence to the first alternative that could match, then either of those trees would be valid interpretations of your input (and means the grammar is technically ambiguous).

However, when there are two alternatives that could be used to match your input, then ANTLR will use the first alternative to resolve the ambiguity, in this case establishing operator precedence, so typically you would put the multiplication/division operator before the addition/subtraction, since that would be the traditional order of operations:

grammar Precedence;
root: expr EOF;

expr
    : expr (' '|'-') expr
    | expr ('*' | '/') expr
    | Atom
    ;

Atom: [0-9] ;
WHITESPACE: [ \t\r\n] -> skip;

Most grammar authors will just put them in precedence order, but things like Atoms or parenthesized exprs won’t really care about the order since there’s only a single alternative that could be used.