Difference between Fourier Space and Real-Space coordinates from a image?-CodePudding

I'm writing a code in Python about phase unwrapping with noise regard a paper published. I have a raw data phase for interferometry [-pi,pi] and I want to unwrap this, but I look data and it has noise in some points.

My trouble with this FFT is I'm very confuse with the difference between (x,y) coordinates from original image and (p,q) coordinates from Fourier Transform (Look the image that I include). When I make a Fourier transform to a image, the pixel coordinates change?

Besides, for the position (0,0) in Fourier coordinates, I will have a 0 as result. How I can handle the zero division?

This is the algorithm:

algorithm

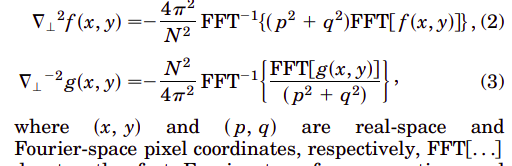
PS: The paper that I get the algorithm is this: https://sci-hub.se/https://doi.org/10.1364/OL.28.001194

CodePudding user response：

The coordinates p and q can be obtained through numpy.fft.fftfreq if FFT(f(x,y)) is obtained through np.fft.fft.

I'd have to read the paper to make sure I understand their definition of p and q. Here I assume they are integer values (because of how they are used, I think this is correct, but I might be wrong!). I'm also assuming that N is the size of the image f(x,y) along both axes. If these assumptions are correct, then you need to set

f = np.fft.fftfreq(N, 1/N)
p = f[:,None]
q = f[None,:]

(The indexing operations to obtain p and q there create 2D arrays where the values run along the one row or one column, respectively.)

Now Broadcasting then allows the operations to produce the right results:

tmp = (p**2   q**2) * np.fft.fft2(f)
out = -(2 * np.pi / N)**2 * np.fft.ifft2(tmp)

(and similarly for the 2nd expression.)