I've been wondering what a complete, all-encompassing context for instance Functor (f :.: g) would be. The immediate thought that pops into my head is:

newtype (f :.: g) a = Comp (f (g a))
instance (Functor f, Functor g) => Functor (f :.: g) where
    fmap f (Comp x) = Comp (fmap (fmap f) x)

But then, two contravariant functors would also compose to be covariant, like so:

instance (Contravariant f, Contravariant g) => Functor (f :.: g) where
    fmap f (Comp x) = Comp (contramap (contramap f) x)

Already not a promising beginning. However, I've also noticed that technically, f and g don't even have to have kind * -> * -- the only requirement for f :.: g :: * -> * is that f :: k -> * and g :: * -> k for some k. This means that non-functor types could compose to be functors, e.g.

newtype Fix f = Fix (f (Fix f))
instance Functor (Fix :.: (,)) where
    fmap f (Comp x) = Comp (go x) where
        go (Fix (x,xs)) = Fix (f x,go xs)

Fix :.: (,) is isomorphic to the Stream type:

data Stream a = a :> Stream a

so this does seem to be a non-trivial issue. This got me thinking -- if Haskell's Functor typeclass represents categorical functors from Hask to Hask, does that mean types like Fix and (,) could be functors working on some other categories? What would those categories be?

CodePudding user response：

Yes, and we can read off exactly what sense that is from the shape of the constructor. Let's look at (,) first.

The `(,)` Functor

(,) :: * -> * -> *

This takes two types and produces a type. Up to isomorphism, this is equivalent to

(,) :: (*, *) -> *

i.e. we might as well uncurry the function and take both arguments at once. So (,) can be viewed as a functor for Hask × Hask to Hask, where Hask × Hask is the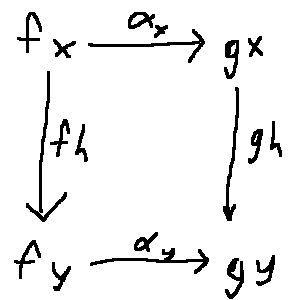

Haskell doesn't really have a built-in type for natural transformations. With Rank-N types, we can write the correct shape

(forall a. f a -> g a)

This is the shape of a natural transformation, but of course we haven't verified the coherence property. So we'll just have to trust that it satisfies that property.

With all of this abstract nonsense in mind, if Fix is going to be a functor from Hask ^ Hask to Hask, it should take a natural transformation to an ordinary Haskell function, and it should have the following shape.

fixmap :: (Functor f, Functor g) => (forall a. f a -> g a) -> Fix f -> Fix g

Once we have this type, we can write the implementation fairly easily.

fixmap h (Fix inner) = Fix (h . fmap (fixmap h) $ inner)

or, equivalently (by the rules of natural transformations),

fixmap h (Fix inner) = Fix (fmap (fixmap h) . h $ inner)

I'm not aware of an idiomatic name for this shape of functor, nor am I aware of a typeclass that encompasses it, but of course nothing stops you from making it yourself.

The (,) Functor

The `(,)` Functor