time complexity of finding 2d peak with greedy ascent algorithm-CodePudding

*there are just one peak

the textbook im studying says the time complexity of greedy ascent algorithm is O(nm) and O(n^2) when m=n. So it means in the worst case, I have to visit all elements of the 2d array.

But I think that case is only when the row or column is 1, and the elements are sorted, so if I choose the minimum element I have to visit all element to get to peak.

At that point, I can't understand that, when n=m, the time complexity is O(n^2).

If n=m=1, it would take O(1), but saying that as O(n^2) is kind of meaningless.

In the other case where n=m and n>1 , isn't it possible to take O(n^2)? If there are none of those, then isn't O(n^2) not the right complexity?

I think O(n m) might be the right complexity becuase the worst case is when the starting point is (0,0) and the peak is at (n,m). So to get to the peak, I have to move verticaly n time, horizentaly m time.

Where am I understanding wrong?

*The point of my question is, I think defining the complexity at the case n=m as O(n^2) based on O(nm) is wrong. And the right complexity is O(n m)=O(2n)=O(n)

CodePudding user response：

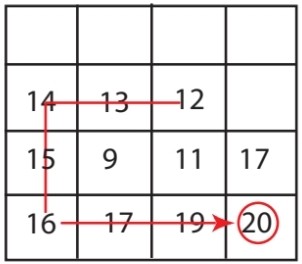
You can easily construct a case where you need to visit at least n*m/2 elements: put the maximum in the bottom-right corner, then follow a zigzagging path, putting an element slightly less than the previous on each traversed space. The path goes all the way to the left, then up two, then all the way to the right, and so on until you reach the top-left or top-right corner. Put a minimum element in all other spaces.

For n=m=4, it looks like this:

If you happen to pick the 1, you need to go through 10 > n*m/2 elements.

For n=4 and m=5:

 1  2  3  4
 0  0  0  5
 9  8  7  6
10  0  0  0
11 12 13 14

Here you need to go through 14 > n*m/2 elements.

So in the worst case, this is O(n*m/2) = O(nm).