I need an algorithm to quickly determine wether given 2D polygon arbitrarily translated intersects given rounded rectangle.
We're given a polygon with N vertices and dimensions of the rounded rectangle (lenghts of sides and radius of corners). We would like to answer many question of type does the polygon with translation (dx,dy) intersect the rounded rectangle. We're allowed to do arbitrary precomputation on the polygon.
When radius of the corners rectangle is 0, there is trivial constant time algorithm - it's enough to compute an AABB of the polygon, and then in few comparisons check if, after translation, it intersects the rectangle.
When the radius is >0 the problem seems much harder. The fact that there seems to be potentially an infinite number of "bounding rounded rectangles" suggests that there is no constant-time algorithm that can check for the intersection. But maybe I'm missing something.
Do you know by any change any sublinear algorithm for checking if a polygon intersects a rounded rectangle?
CodePudding user response:
If preprocessing of the polygon is allowed, an efficient solution is possible:
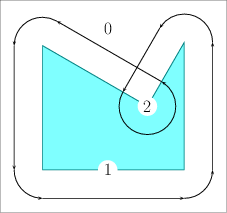
build the Minkowski sum of the polygon and rounded rectangle; this is a curvilinear polygon;
every translation of the polygon wrt the rectangle corresponds to a point wrt the Minkowski sum;
decompose the curvilinear polygon in slabs;
you can perform location of an arbitrary point in that decomposition in time O(log(N)), and this is optimal.
Below, the sum of two polygons and of a concave polygon with a disk (the loop must be excluded). This generalizes to a rounded rectangle.
To locate a point, you identify the containing slab by dichotomic search. Then inside a slab, you can identify the containing curvilinear trapezoid (delimited by line segments or circular arcs) by a second dichotomic search.
If you have few polygons, with a simple shape, you can do the preprocessing by hand. Otherwise, the Minkowski sum and slab decomposition are a little painful.
CodePudding user response:
Let x1, x2, y1, y2 be the coordinates of the AABB of the rounded rectangle, with x1 < x2 and y1 < y2, and let R be the radius (of the quarter-circles).
Here is how I would handle the collision detection. Optionally, you can of course check for collision with the AABBs of both objects first, to reject early. Then, for each line in the polygon:
- check for intersection with the rectangle made from the following points:
(x1, y1 R),(x1, y2-R),(x2, y1 R),(x2, y2-R) - check for intersection with the rectangle made from the following points:
(x1 R, y1),(x1 R, y2),(x2-R, y1),(x2-R, y2) - check for intersection with each of the circles in the corners, that is the circles or radius R and centers:
(x1 R, y1 R),(x1 R, y2-R),(x2-R, y1 R),(x2-R, y2-R)
If any of these three checks gives an intersection, then the polygon intersects the rounded rectangle or is completely inside. Of course, you can check whether a point of the polygon is outside the rounded rectangle using the same method (you can easily do it at the same time as the intersection checks). Because a rounded rectangle is a convex shape, this is sufficient to say that the polygon is not completely inside.
That's O(N) where N is the number of sides of your polygon. If that's the complexity you are thinking of when you say "constant-time", then I don't believe there is any kind of preprocessing that can help go below O(N) in the general case.