Why does Opencv Imgproc.minAreaRect give different results for the same points (that make up an asym-CodePudding

When I run:

    @Test
    public void funkyTriangleContour2_forStack_works() {
        final var points = new Point[]{new Point(), new Point(1, 0), new Point(1, 2)};
        final var contour = new MatOfPoint2f(points);

        final var minRect = Imgproc.minAreaRect(contour);


        System.out.println("center: "   minRect.center);
        System.out.println("rotation: "   minRect.angle);
        System.out.println("width: "   minRect.size.width   " height: "   minRect.size.height);


        assertThat(minRect.size.area(), is(lessThan(2.0)));
        assertThat(minRect.size.area(), is(greaterThan(1.0)));
    }

it passes and gives:

center: {0.9000000953674316, 0.800000011920929}
rotation: 63.43495178222656
width: 2.2360680103302 height: 0.8944271206855774

But when I change the order of the points which should not change the min-bounding rect I get a different answer:

    @Test
    public void funkyTriangleContour2_forStack_fails() {
        final var points = new Point[]{new Point(1, 0), new Point(1, 2), new Point()};
        final var contour = new MatOfPoint2f(points);

        final var minRect = Imgproc.minAreaRect(contour);

        System.out.println("center: "   minRect.center);
        System.out.println("rotation: "   minRect.angle);
        System.out.println("width: "   minRect.size.width   " height: "   minRect.size.height);


        assertThat(minRect.size.area(), is(lessThan(2.0)));
        assertThat(minRect.size.area(), is(greaterThan(1.0)));
    }

it fails and gives:

center: {0.5, 1.0}
rotation: 90.0
width: 2.0 height: 1.0

My understanding of the routine is that it gives a bounding rect that may be rotated to keep it small that encloses all the points, so the order of the points should not matter. Even if it refers to a contour, rotating the points should not change the result.

Any idea why this does this?

Thank you

CodePudding user response：

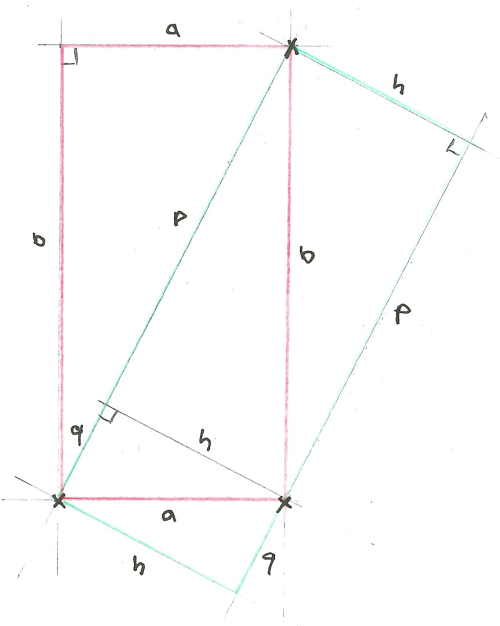
There actually are two distinct solutions to this problem, shown in the following sketch:

Where h is the altitude to the hypotenuse p q, and its formula is h = (a * b) / (p q).

If we rearrange that slightly, we get h * (p q) = a * b -- the left hand side now represents the area of the green rectangle, the right hand side the area of the red rectangle. Therefore, both of the rectangles have the same area.

The discrepancy you see is going to be caused by the limited accuracy of floating point numbers.

I haven't studied the algorithm, but it appears that the order in which points are provided determines which of the potentially multiple solutions gets selected, and in turn whether and how much of an error gets accumulated (or simply just caused by inability to represent all the parameters of the solution accurately).

In fact, it turns out that the algorithm was modified several times in the history of OpenCV -- I was able to get 3 different results from 3 different versions of OpenCV, for the exact same points in the same order. Part of the problem here is also that there are multiple ways how to describe the same rectangle with the 5-tuple OpenCV uses (I see 4 by just playing with width, height and rotation angle).