Align a 3D line A to the line B-CodePudding

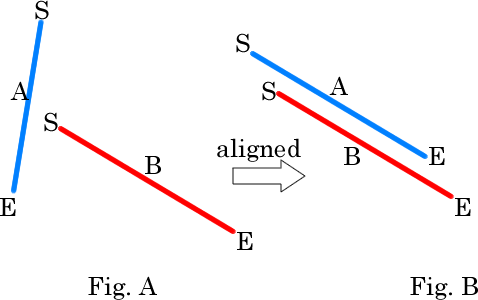
I want to align a line A (blue), which is defined with a 3D start (S) and 3D end point (E) to the other 3D line B (red), so that the line A (does not matter, how it is originally positioned) is parallel to the line B, as shown in Fig.B

I know that I have to calculate the angle between two them for that I do:

def calcAngleBtw2Lines(self, vec1S, vec1E, vec2S, vec2E):

    # Substract the end point (E) from the start point (S) of the line
    vec1 = np.subtract(vec1E, vec1S)
    vec2 = np.subtract(vec2E, vec2S)

    # Dot product to get the cosine of the rotation angle
    dotProduct = np.dot(vec1, vec2)

    # Normalize the vectors to find the unit vectors
    vec1Unit = np.linalg.norm(vec1)
    vec2Unit = np.linalg.norm(vec2)

    # Find the angle between vectors
    angle = np.degrees(np.arccos(dotProduct / (vec1Unit * vec2Unit)))
    print("angle: ", angle)

    return np.round(angle, 1)

But I am not sure, whether the steps are correct. If they are parallel to each other, the angle between them should be 0

Edit: The length of both lines are equal. The line B is stationary. To make line A parallel to the B, the S and E of A can be moved at the same time.

CodePudding user response：

Ok, here's a working answer. Note that if A and B have the same lengths, part of the code is unnecessary (but I'll leave it anyway to make it more portable):

import numpy as np

def makeAparalleltoB(pointSA, pointEA, pointSB, pointEB):
# pointSA... are np.arrays of the 3 coordinates

    # Calculating the coordinates of the vectors
    vecA = pointEA - pointSA
    vecB = pointEB - pointSB

    # Calculating the lengths of the vectors
    # Unnecessary if we know that A and B have the same lengths
    vecANorm = np.linalg.norm(vecA)
    vecBNorm = np.linalg.norm(vecB)

    # Calculating the coordinates of a vector collinear to B, of the same length as A
    newvecA = vecB * vecANorm/vecBNorm

    # Returning new coordinates for the endpoint of A
    return pointSA   newvecA

Example:

a = np.array([1,1,1])
b = np.array([2,3,4])
c = np.array([0,0,0])
d = np.array([1,1,1])

print(makeAparalleltoB(a, b, c, d))

# [3.1602469 3.1602469 3.1602469]

If we know that A and B have the same length, then it's even simpler: we simply make it so SB, EB, EA, SA is a parallelogram:

newpointEA = pointSA   pointEB - pointSB