How to remove duplicate node's children (by tagging the node) in R?-CodePudding

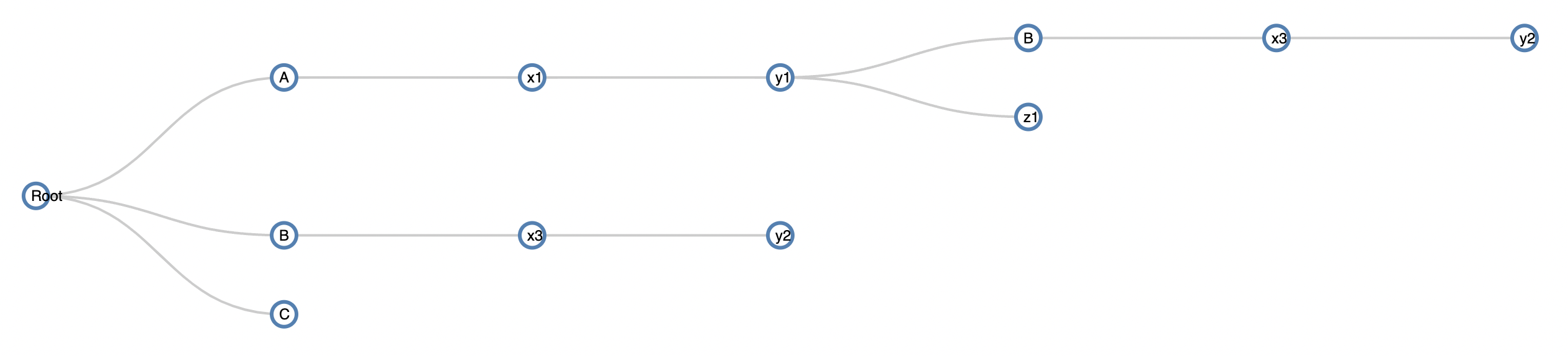
Here is an reproducible data example

library(data.table)
testDT = fread(
"from   to
Root    A
A   x1
x1  y1
y1  z1
y1  B
Root    B
B   x3
x3  y2
Root    C")

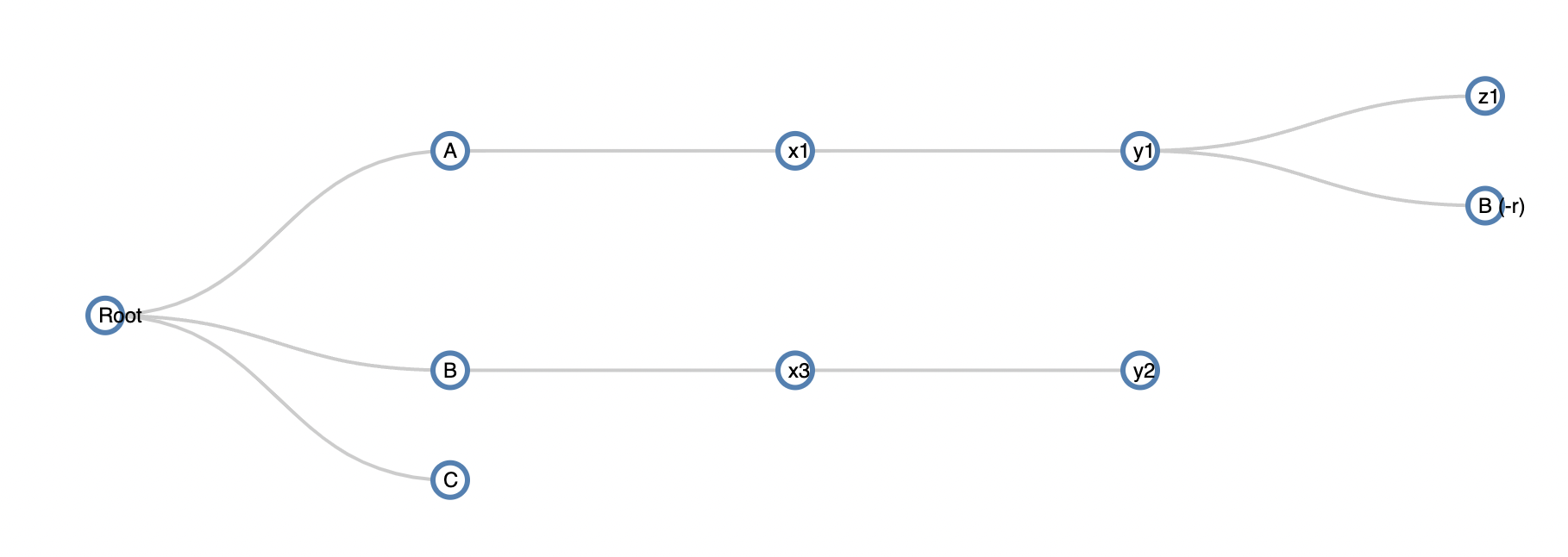
An example visualization of the data:

As you see, hierarchically, the same node B at level1 appears as a child of node y1. What I would like to do is remove if the repeating node B has children and tag it. The output I want is:

The output table that i desired:

| from        | to            |
|-------------|---------------|
|     Root    |     A         |
|     A       |     x1        |
|     x1      |     y1        |
|     y1      |     z1        |
|     y1      |     B (-r)    |
|     Root    |     B         |
|     B       |     x3        |
|     x3      |     y2        |
|     Root    |     C         |

I had prepared a question to remove the node that caused the recursive build and they provided a solution thanks. However, this solution completely deletes node B connected to y1 against my will.

CodePudding user response：

I couldn't come up with a simple igraph solution as all the traverse functions in igraph will not visit the same node twice. Therefore I wrote a bfs algorithm that will keep track of edges where the child has already been visited.

library(purrr)
library(igraph)
library(dplyr)

G <- graph_from_data_frame(testDT)

stack <- 'Root'
traversed <- c()
edges <- data.frame(from = c(), to = c(), traversed = c())

while(length(stack) > 0) {
    el <- stack[1]
    stack <- stack[-1]
    children <- adjacent_vertices(G, el, mode = "out" )[[1]] |>
        map_chr(~names(V(G)[.x]))
    if(!el %in% traversed) {
        traversed <- c(el, traversed)
        if (length(children) > 0) {
            edges_ <- data.frame(from = el, to = children) |>
                mutate(traversed = to %in% traversed)) 
            stack <- c(stack, edges_ |> filter(!traversed) |> pull(to))
            edges <- rbind(edges_, edges)
        }
    }
}

edges

##>    from to traversed
##> B    y1  B      TRUE
##> z1   y1 z1     FALSE
##> y2   x3 y2     FALSE
##> y1   x1 y1     FALSE
##> x3    B x3     FALSE
##> x1    A x1     FALSE
##> A  Root  A     FALSE
##> B1 Root  B     FALSE
##> C  Root  C     FALSE

Then, with simple data manipulation you can obtain the desired format.

edges |>
    mutate(to = ifelse(traversed,
                       paste(to, "(-r)"),
                       to),
           .keep = "unused")

##>      from     to
##> B    y1 B (-r)
##> z1   y1     z1
##> y2   x3     y2
##> y1   x1     y1
##> x3    B     x3
##> x1    A     x1
##> A  Root      A
##> B1 Root      B
##> C  Root      C