Does the order of points matter in spline interpolation in MatLab?-CodePudding

I am using MatLab to pick the data point with my mouse and then fit it with a spline. I found the following function could do the job

[xy, spcv] = getcurve()

it returns the x & y of the points I picked with a mouse

x = [ -0.8103   -0.6740   -0.5599   -0.5120   -0.4936   -0.4530   -0.4494   -0.4494   -0.4494   -0.4751 -0.5157   -0.6409   -0.6667   -0.7772   -0.7772   -0.6998   -0.5304   -0.4641   -0.2431    0.0110 0.1142    0.1989    0.2836    0.3499    0.3499    0.4125    0.5267]
y = [0.8621    0.8388    0.7640    0.7547    0.7266    0.6472    0.5911    0.5257    0.4696    0.3668 0.2967    0.2360    0.2220    0.0724   -0.1472   -0.1939   -0.2874   -0.4743   -0.5304   -0.5257 -0.4930   -0.3668   -0.2967   -0.2593   -0.2593   -0.2827   -0.3715

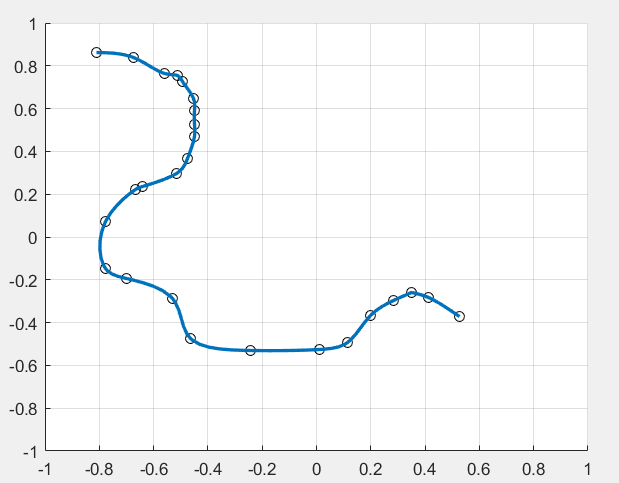
plotting the spline spcv returned by getcurve(), I get the following figure

By reading the code of getcurve, I see that it uses cscvn to return a parametric `natural' cubic spline that interpolates to the given points. It may be the reason why the curve is passing all given points instead of the best-fit curve. I would like to replace it with a cubic smoothing spline as below

sp = spaps(x, y, 0.);
xx = -1:0.01:2;
plot(xx, fnval(sp, xx), 'b', 'linewidth', 2); hold on;
plot(x, y, 'ko');

which gives me something strange as follow

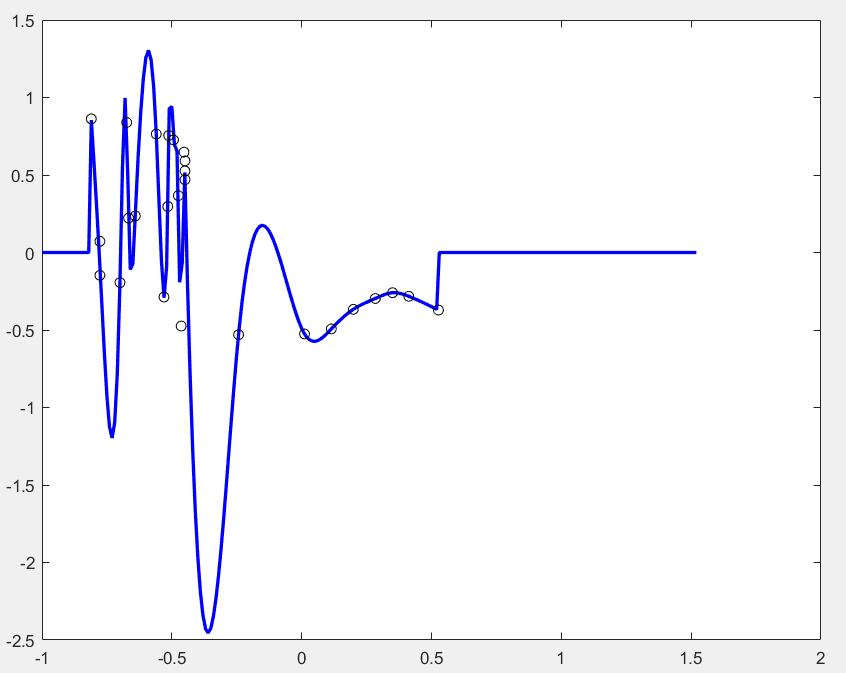
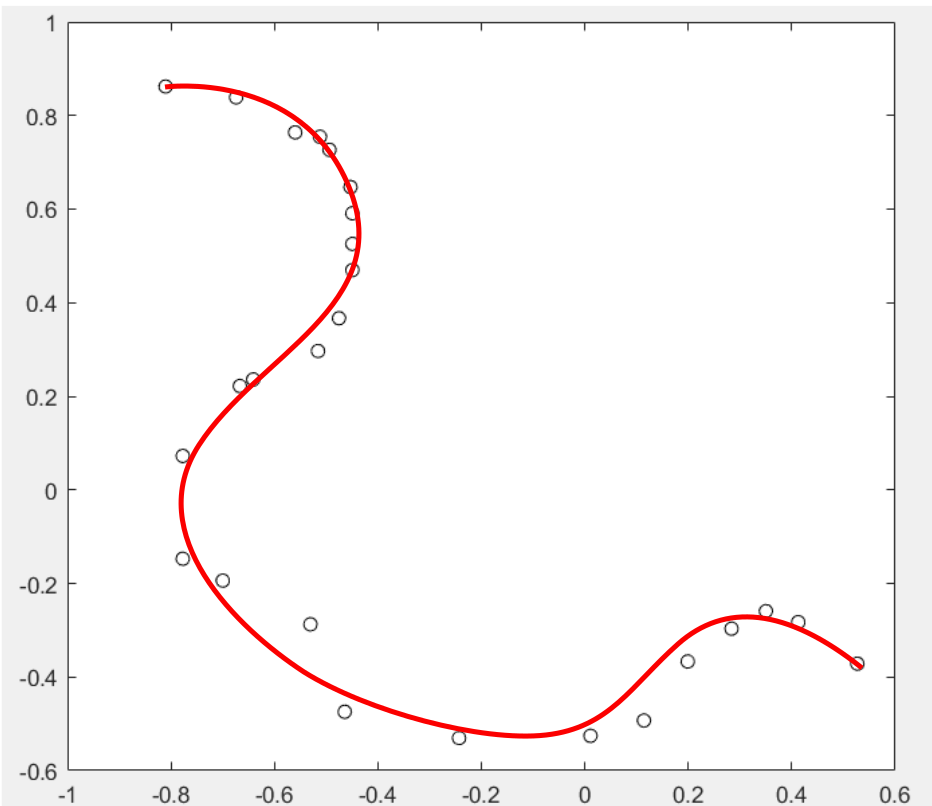
It looks like it is trying to fit the data points from small x to big x instead of the order given by the data sequence. I am expecting a smooth curve in red as below (I draw it by hand)

I am looking for a solution that I can replace cscvn with spaps in getcurve and keep the correct order. Thanks.

CodePudding user response：

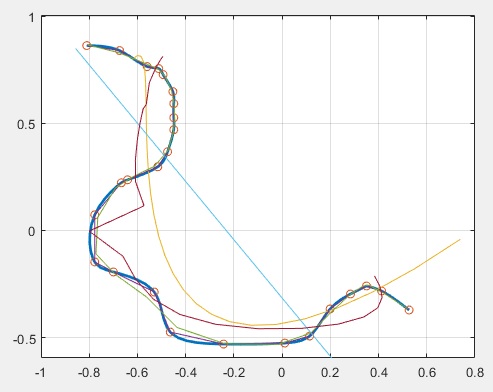
1.- To interpolate curves that fold back you have to parametrize x and y

x = [ -0.8103   -0.6740   -0.5599   -0.5120   -0.4936   -0.4530   -0.4494   -0.4494   -0.4494   -0.4751 -0.5157   -0.6409   -0.6667   -0.7772   -0.7772   -0.6998   -0.5304   -0.4641   -0.2431    0.0110 0.1142    0.1989    0.2836    0.3499    0.3499    0.4125    0.5267];
y = [0.8621    0.8388    0.7640    0.7547    0.7266    0.6472    0.5911    0.5257    0.4696    0.3668 0.2967    0.2360    0.2220    0.0724   -0.1472   -0.1939   -0.2874   -0.4743   -0.5304   -0.5257 -0.4930   -0.3668   -0.2967   -0.2593   -0.2593   -0.2827   -0.3715];

figure(1)
ax1=gca
fnplt(cscvn([x;y])); hold(ax1,'on');
plot(ax1,x,y,'o');
grid on

sp = spaps(x, y, 0.);
xx = -1:0.01:2;
figure(2)
plot(xx, fnval(sp, xx), 'b', 'linewidth', 2); hold on;
plot(x, y, 'ko'); grid on


nx=[1:numel(x)];ny=[1:numel(y)];

fx=fit(nx',x','poly3','Normalize','on','Robust','Bisquare')
fy=fit(ny',y','poly3','Normalize','on','Robust','Bisquare')
plot(ax1,fx(nx),fy(ny))

f2x=fit(nx',x','cubicinterp','Normalize','on')
f2y=fit(ny',y','cubicinterp','Normalize','on')
plot(ax1,f2x(nx),f2y(ny))

f3x=fit(nx',x','smoothingspline','Normalize','on')
f3y=fit(ny',y','smoothingspline','Normalize','on')
plot(ax1,f3x(nx),f3y(ny))

f4x=fit(nx',x','poly1','Normalize','on')
f4y=fit(ny',y','poly1','Normalize','on')
plot(ax1,f4x(nx),f4y(ny))

f5x=fit(nx',x','poly11','Normalize','on')
f5y=fit(ny',y','poly11','Normalize','on')
plot(ax1,f5x(nx),f5y(ny))

f6x=fit(nx',x','rat33','Normalize','on')
f6y=fit(ny',y','rat33','Normalize','on')
plot(ax1,f6x(nx),f6y(ny))

2.- Note that nx and ny have same amount of samples as x and y.

If you interpolate x over nx and y over ny and then apply fit the resulting curve will get closer to all points in the way you asked for.