Fitting Hyperbolic Cosine curve in Python-CodePudding

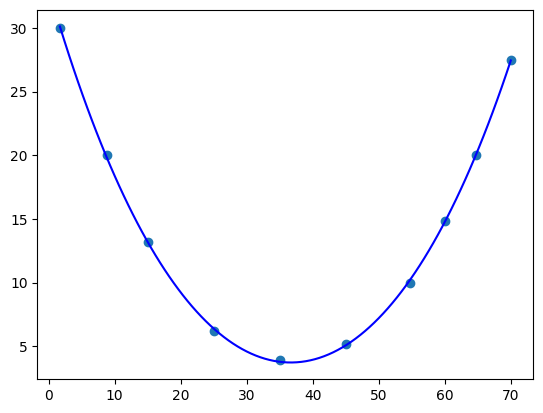
Now I want to fit in one bump of hyperbolic cosine curve into the following X and Y data:

xData = np.array([1.7, 8.8, 15, 25, 35, 45, 54.8, 60, 64.7, 70])
yData = np.array([30, 20, 13.2, 6.2, 3.9, 5.2, 10, 14.8, 20, 27.5])

Here's what I have done so far but I am not getting the expected result and I have no idea what I am doing wrong:

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import scipy.interpolate as inp

xData = np.array([1.7, 8.8, 15, 25, 35, 45, 54.8, 60, 64.7, 70])
yData = np.array([30, 20, 13.2, 6.2, 3.9, 5.2, 10, 14.8, 20, 27.5])

def model_hcosine(x, a, b, c):
    return a * np.cosh(x/b)   c

poptcosh, pcovcosh = curve_fit(model_hcosine, xData, yData, p0=[min(yData), max(xData), max(yData)])

aapopt, bbopt, cccopt = poptcosh
xCoshModel = np.linspace(min(xData), max(xData), 100)
yCoshModel = model_hcosine(xCoshModel, aapopt, bbopt, cccopt)

plt.scatter(xData, yData)
plt.plot(xCoshModel, yCoshModel, 'b-')

plt.show()

CodePudding user response：

@WarrenWeckesser is correct, you need to account for the translation within the cosh function. You can add an additional parameter d to the model, and give it an initial condition of 0 in the optimizer. Then you unpack the optimal coefficients and plug them into the model before plotting. I got the following

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import scipy.interpolate as inp

xData = np.array([1.7, 8.8, 15, 25, 35, 45, 54.8, 60, 64.7, 70])
yData = np.array([30, 20, 13.2, 6.2, 3.9, 5.2, 10, 14.8, 20, 27.5])

def model_hcosine(x, a, b, c, d):
    return a * np.cosh((x-d)/b)   c

poptcosh, pcovcosh = curve_fit(model_hcosine, xData, yData, p0=[min(yData), max(xData), max(yData), 0])

aapopt, bbopt, cccopt, ddopt = poptcosh
xCoshModel = np.linspace(min(xData), max(xData), 100)
yCoshModel = model_hcosine(xCoshModel, aapopt, bbopt, cccopt, ddopt)

plt.scatter(xData, yData)
plt.plot(xCoshModel, yCoshModel, 'b-')

plt.show()

CodePudding user response：

This post is not an answer but a comment too long to be edited in the comments section.

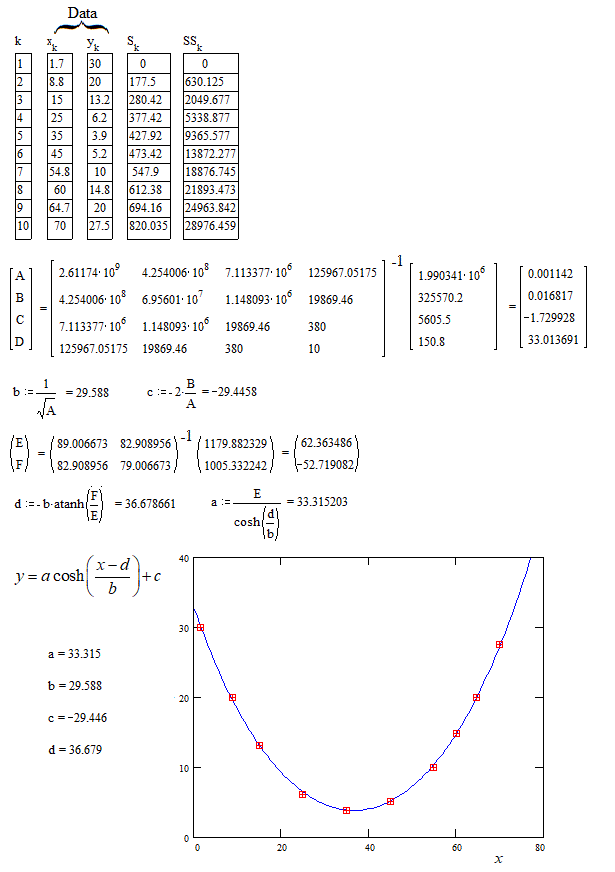
For information :

The usual method of fitting (such as in Python) involves an iterative process starting from "guessed" values of the parameters which must be not too far from the unknown exact values.

An unusual method exists not iterative and not requiring initial values to start the calculus. The application to the case of the hyperbolic cosine function is shown below with a numerical example.

The above method consists in a linear fitting of an integral equation to which the hyperbolic cosine is solution. For general explanation see https://fr.scribd.com/doc/14674814/Regressions-et-equations-integrales . The case of hyperbolic cosine isn't explicitly treated in this paper. That is why the details are given above.

Note : If some particular criteria of fitting is specified ( MLSE, MLSAE, MLSRE or other) one cannot avoid nonlinear regression. Then the approximate values of the parameters found above are very good values to start the iterative process in expecting a better reliability.