#include
#include
using namespace std;
Int main ()
{
Int m, n, s=1, I, j, a=0;
While (the scanf (" % d % d ", & amp; M, & amp; N)!=(EOF)
{
If (m==0 & amp; & N==0)
{
break;
}
If (m> N)
{
int t;
T=m;
M=n;
N=t;
}
For (I=m; i<=n; I++)
{
Float TMP.
TMP=SQRT (I);
For (j=2; j<=TMP; J++)
{
If (I % j==0)
{
If (j==I/j)
{
S=s + j;
}
The else
{
S=s + + I/j j;
}
}
}
if(i!=1 & amp; & I==s)
{
Printf (" % d ", I);
A=a + 1;
}
S=1;
}
If (a==0)
{
Printf (" \ n ");
a=0;
}
The else
{
printf("\n");
}
}
return 0;
}
CodePudding user response:
Is optimized, and think there is still room for optimization?CodePudding user response:
At least see the program and to optimize clear,CodePudding user response:
A number of factors set is divisible divisor and the quotient set,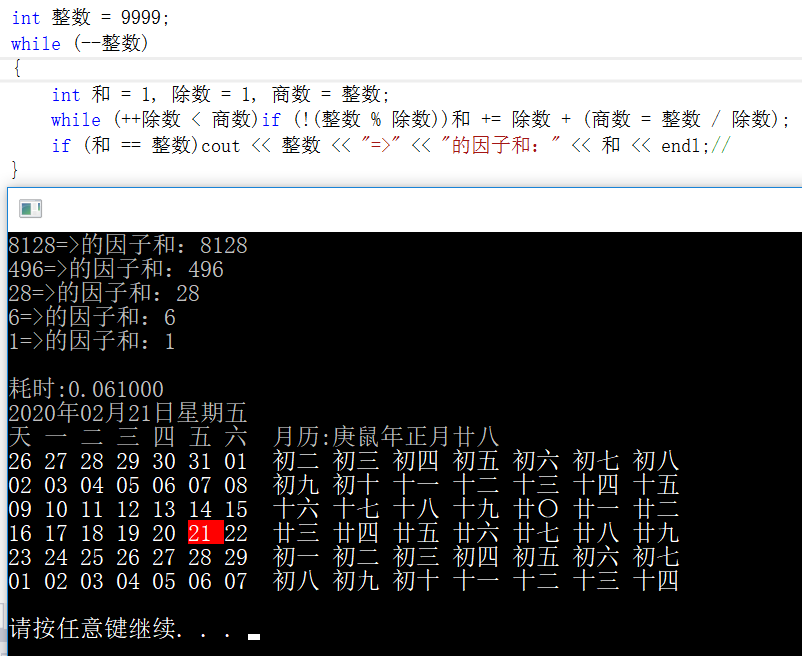
The optimization, don't have to write so much code,
CodePudding user response:
And +=divisor + (=integer/divisor) this is not rightCode of the building Lord, don't want to compare divisor and traders are the same, the same word can only add a
Code is the core of the building Lord, is the dual cycle, other places are not important point
Somewhere else, after all, just to perform a double loop in the case of m and n the number is larger, just can have value
Not to mention to assembly language implementation, only see algorithm
Here really have a place can be optimized:
If (j== I/j
{
S=s + j;
}
The else
{
S=s + j + I/j ;
}
Plan A
Int t=I/j;
If (t==j) s +=j; The else s +=j + t;
Here the two I/j turned into an
Plan B
If (j * j==I) s +=j; The else s +=j + I/j;
Replace the division with multiplication, division computation is more than the 2 times of multiplication
At the back of the s +=j + I/j; This division or avoid
Considering most of the cases, j * j==I is not established, so I/j this operation is to avoid the risk of small
A and B who is faster, multiplication/division unavailable and t==j/t! Who has a big
between=j
Both A and B, the original two division of high efficiency,
CodePudding user response:
Perfect number did use root as end faster, optimization of the place I yes, problem is in the end use, for some number is not suitable, it is also noticed that just made a validation, the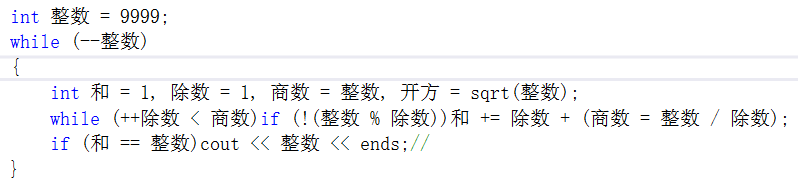
CodePudding user response:
Many with business is relatively close to open,CodePudding user response:

