Sample N points from a set of 3D points that maximizes the minimum distance-CodePudding

Say I have 500 random 3D points represented by a (500, 3) array:

import numpy as np

np.random.seed(99)
points = np.random.uniform(0, 10, (500, 3))

Now I want to sample n = 20 points from these 500 points, so that the minimum value of all pairwise distances is the largest. I am using a greedy approach that samples the point that maximizes the minimum distance each time. Below is my Python implementation:

from scipy.spatial import distance_matrix

def sample_n_points(points, n):
    sampled_points = [points[0]]
    remained_points = points[1:]
    n_sampled = 1

    while n_sampled < n:
        min_dists = distance_matrix(remained_points, sampled_points).min(axis=1)
        imax = np.argmax(min_dists)
        sampled_points.append(remained_points[imax])
        np.delete(remained_points, (imax), axis=0)
        n_sampled  = 1

    return np.asarray(sampled_points)

print(sample_n_points(points, n=20))

Output:

[[6.72278559 4.88078399 8.25495174]
 [1.01317279 9.74063145 0.15102072]
 [5.21672436 0.39259574 0.1069965 ]
 [9.89383494 9.77095442 1.15681204]
 [0.77144184 9.99325146 9.8976312 ]
 [0.04558333 2.34842151 5.25634324]
 [9.58126175 0.57371576 5.01765991]
 [9.93010888 9.959526   9.18606297]
 [5.27648557 9.93960401 4.82093673]
 [2.97622499 0.46695721 9.90627399]
 [0.28351187 3.64220133 0.06793617]
 [6.27527665 5.58177254 0.3544929 ]
 [0.4861886  7.45547887 5.342708  ]
 [0.83203965 5.00400167 9.40102603]
 [5.21120971 2.89966623 4.24236342]
 [9.18165946 0.26450445 9.58031481]
 [5.47605481 9.4493094  9.94331621]
 [9.31058632 6.36970353 5.33362741]
 [9.47554604 2.31761252 1.53774694]
 [3.99460408 6.17908899 6.00786122]]

However, by using this code, an optimal solution is not guaranteed. The most obvious "mistake" of my code is that it always starts by sampling the first point. Of course I can run my code using each point as the starting point and finally take the one that maximizes the minimum distance, but even that won't give the optimal solution. The points are very apart from each other in the beginning, but are forced to be close to each other as more points are sampled. After some thought, I realize this problem essentially becomes

finding the subset in a set of 3D points that most evenly distributed.

I want to know if there is any algorithm that can find the optimal solution or give a good approximation relatively fast?

Edit

The decision problem version of this optimization problem would be:

given a distance threshold t, whether it is possible to find a subset of n points such that every pair of points in the subset are at least t apart.

In a graph point of view, this can be intepreted as

finding an independent set in a Euclidean graph, where points v1, v2 have an edge between them if the pairwise distance d(v1,v2) ≤ t.

If we can solve this decision problem, then the optimization problem can also be solved by a binary search on the threshold t.

CodePudding user response：

Hopefully I have understood your requirements.

Following on from your start:

from scipy.spatial import distance_matrix
import numpy as np

np.random.seed(99)
points = np.random.uniform(0, 10, (500, 3))

You should get the distance between all points and sort on the distance:

# get distances between all points
d = distance_matrix(points, points)
# zero the identical upper triangle
dt = np.tril(d)
# list the distances and their indexes
dtv = [(dt[i, j], i, j) for (i, j) in np.argwhere(dt > 0)]
# sort the list
dtvs = sorted(dtv, key=lambda x: x[0], reverse=True)

Then you can grow a set to get the 20 indices to points that contribute to the greatest distances.

Edit to limit the result to k unique point indices.

kpoint_index = set()
k = 20
i = 0

for p in (j for i in dtvs for j in i[1:]):
    kpoint_index.add(p)
    if len(kpoint_index) == k:
        break

print("index to points:", kpoint_index)

giving:

index to points: {393, 11, 282, 415, 160, 302, 189, 319, 194, 453, 73, 74, 459, 335, 469, 221, 103, 232, 236, 383}

This runs pretty quickly - but I did not time it.

CodePudding user response：

After some illuminating comments, I recognise the exact solution is intractable for even moderate problem sizes.

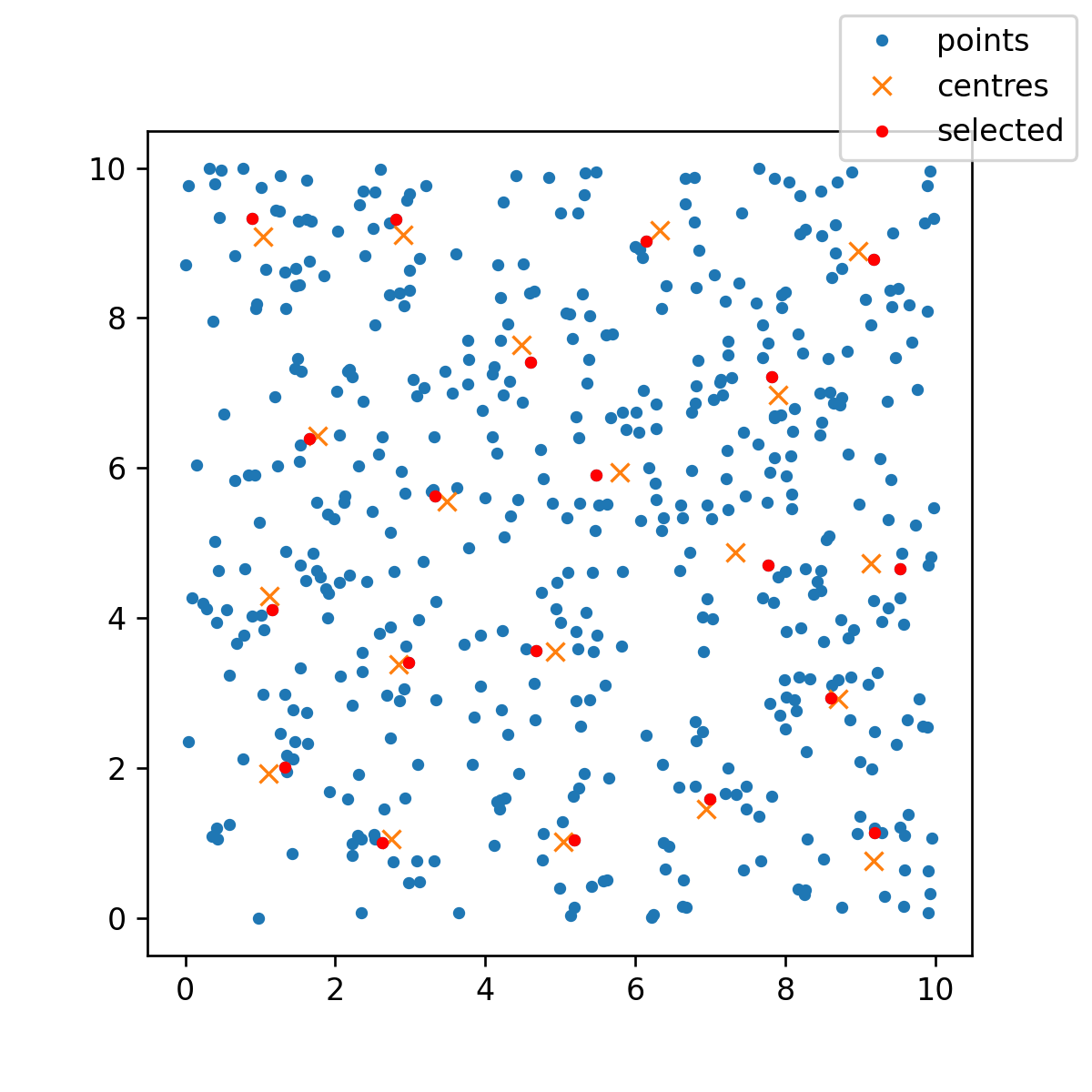
One possible approximate solution uses K-means clustering. Here is an example in 2D so I can include a plot.

np.random.seed(99)
n = 500
k = 20
pts2D = np.random.uniform(0, 10, (n, 2))

kmeans = KMeans(n_clusters=k, random_state=0).fit(pts2D)
labels = kmeans.predict(pts2D)
cntr = kmeans.cluster_centers_

Now we can find which of the original points is nearest to each cluster centre:

# indices of nearest points to centres
approx = []

for i, c in enumerate(cntr):
    lab = np.where(labels == i)[0]
    pts = pts2D[lab]
    d = distance_matrix(c[None, ...], pts)
    idx1 = np.argmin(d, axis=1)   1
    idx2 = np.searchsorted(np.cumsum(labels == i), idx1)[0]
    approx.append(idx2)

Then, we can plot the result:

fig, ax = plt.subplots(figsize=(5, 5))
ax.plot(pts2D[:, 0], pts2D[:, 1], '.')
ax.plot(cntr[:, 0], cntr[:, 1], 'x')
ax.plot(pts2D[approx, 0], pts2D[approx, 1], 'r.')
ax.set_aspect("equal")
fig.legend(["points", "centres", "selected"], loc=1)

Finally, if the real points are always uniformly distributed, you could get a good approximation by uniformly placing "centres" and selecting the nearest point to each. There would then be no need for K-means.