I have implemented a function called dijkstra() that returns the shortest path from the origin to the destination. I want to add a modification so that the path passes through a specific node. The result is this:

def checkpoint(G, origin, destination, extra):

    path1 = dijkstra(G,origin,extra)['path'] # returns a list with the path
    path2 = dijkstra(G,extra,destination)['path'] 
    
    path = path1   path2
    
    return path

I have implemented dijkstra with a priority queue, so the complexity is O(E V log(V)).

My question is: Is there another more efficient way to solve this problem? What would be the complexity of the checkpoint function?

CodePudding user response：

If problem permits you to have cycles in your path and there is only one checkpoint. Then your solution can solve the problem without change in the time complexity (although with more number of operations, but not important).
If cycles are not allowed, your solution will fail. Think about the example below:

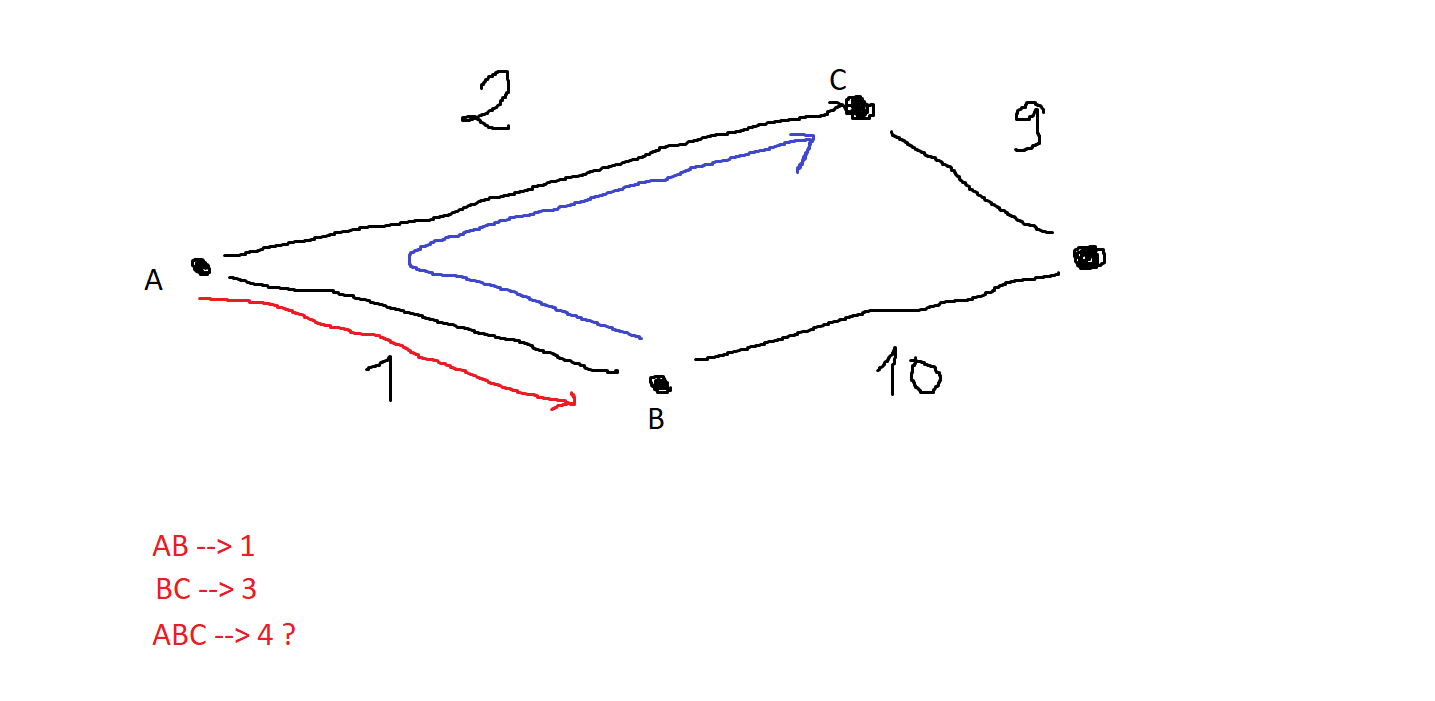
If you try to find a shortest path from A to B, you will get the path with length 1. If you try to find a shortest path from B to C, you will get the path with lenght 3. However, it requires you to go through the point A. Therefore there will be a cycle in your solution.

Solution: Modify your Dijkstra such that first call returns a list of visited nodes, and second call takes these nodes and eliminates them from graph, so that we guarantee that there is no cycle in our paths. However such approach is risky, because we can eliminate the shortest path by not visiting the nodes that were visited in the previous Dijkstra call. Second approach would be doing the same thing reverse:
Call Dijkstra from A to B and return visited nodes
Call Dijkstra from B to C, eliminating visited nodes
Store the length of the path in a variable
Call Dijkstra from B to C and return visited nodes
Call Dijkstra from A to B, eliminating visited nodes
Store the length of the path in a variable
Compare the lengths and return the path associated with the shortest one.

CodePudding user response：

An implementation of Dijkstra's algorithm commonly computes the shortest path to all possible destinations.

This suggest you could:

1. Set the checkpoint as the starting point for the algorithm
2. Run dijkstra once from this starting point
3. Combine the shortest path from the starting point to the checkpoint with the shortest path from the starting point to the destination

This would only work for undirected graphs and assumes that an edge can be used more than once.

You may also find that the implementation will terminate as soon as the destination node is found, so you would need to modify it to only terminate once both final points have been found.