I am trying to determine the phase of two superposed complex plane waves. There are two simple ways of implementing this:

1. The first is to write each as a complex array and add them.
2. The second is to do some math behind the scenes and ask numpy to write the exact result.

The two results do not agree. Here is a MWE:

from pylab import *

x = linspace(0,2*pi)

k1 = 1
k2 = 2

planewave1 = exp(1j*k1*x)
planewave2 = exp(1j*k2*x)

superwave = planewave1   planewave2

rho = 2   2*cos( (k2-k1)*x )
theta = (k1 k2)/2 * x

superwave_theory = sqrt(rho) * exp(1j*theta)

phase_Numpy  = angle(superwave)
phase_theory = angle(superwave_theory) # = theta % pi

These phase angles as calculated by each method disagree:

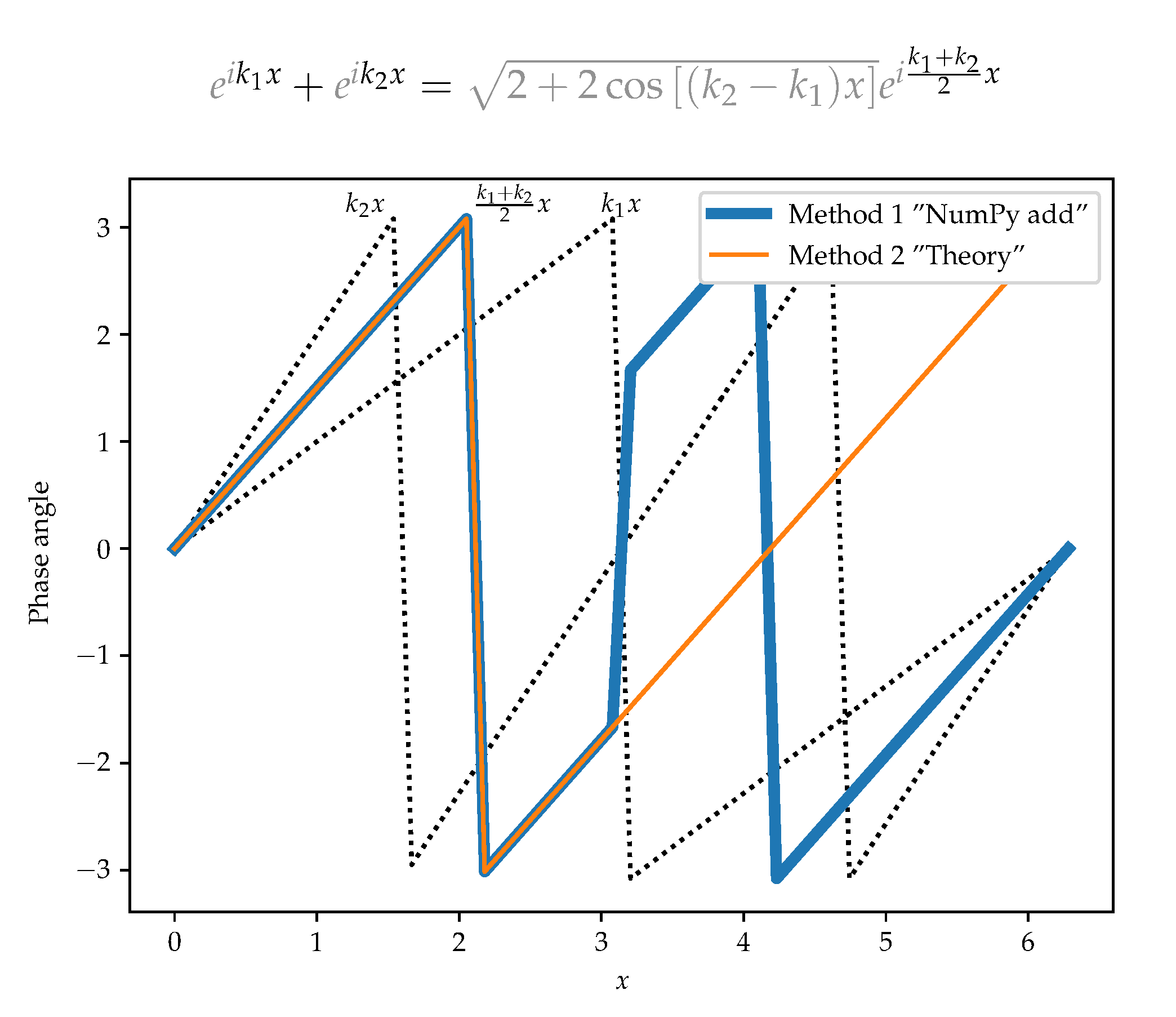
Why do the results disagree?

The theoretical calculation indicates that the phase of the superposed waves is the average of the phase of the individual waves. I have dotted in the phases of the individual plane waves from which we can see that this is correct (the orange line is mid-way between the black dotted lines on the "inside").

Of course the phase angles continue past Pi, but numpy's angle() wraps the result in (-pi,pi].

The two methods agree until the slower plane wave wraps around to -pi. From the plot it is clear that the numpy method (blue line) is midway between the wrapped first phase line and the unwrapped slower phase. This should not happen and gives a result that is off by pi.

To me this seems like a bug in NumPy's handling of complex arithmetic but it is possible that I am misusing the code in some way.

I am using NumPy 1.21.1.

CodePudding user response：

Your formula is not correct for all x. Consider x = 3.5:

In [49]: import cmath, math

In [50]: k1 = 1

In [51]: k2 = 2

In [52]: x = 3.5

Here's the sum of the complex exponentials:

In [53]: cmath.exp(1j*k1*x)   cmath.exp(1j*k2*x)
Out[53]: (-0.18255443294749174 0.3062033710291692j)

Here's your formula:

In [54]: math.sqrt(2   2*math.cos((k2 - k1)*x))*cmath.exp(1j*(k1   k2)*x/2)
Out[54]: (0.18255443294749166-0.3062033710291693j)

Note that the result computed using the formula has the wrong sign (which is equivalent to having a phase that is off by π).

It is true that

(exp(1j*k1*x)   exp(1j*k2*x))**2 = (2   2*cos((k1 - k2)*x))*exp(1j*(k1 k2)*x)

(I wish we had LaTeX here on stackoverflow.) To get your formula, you have to take the square root of both sides, but the complex square root is multivalued. Your formula picks the wrong branch for x > π.