Codecademy Merge sort Algorithm-CodePudding

I am currently taking a code academy course in sorting algorithms with Python, and I'm currently on merge sort. However, the code that is shown seems to contradict the graph they show.

def merge_sort(items):
  if len(items) <= 1:
    return items

  middle_index = len(items) // 2
  left_split = items[:middle_index]
  right_split = items[middle_index:]

  left_sorted = merge_sort(left_split)
  right_sorted = merge_sort(right_split)

  return merge(left_sorted, right_sorted)

def merge(left, right):
  result = []

  while (left and right):
    if left[0] < right[0]:
      result.append(left[0])
      left.pop(0)
    else:
      result.append(right[0])
      right.pop(0)

  if left:
    result  = left
  if right:
    result  = right

  return result

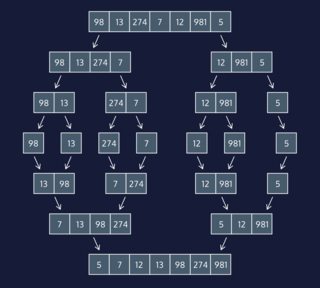
Meanwhile, this is the graph shown to reflect this traversal:

So, the graph is showing me that the way the list is first split is that the left split should be all the numbers from the beginning up to and including the middle index. However, the code is saying that the left split should be all the numbers from the beginning up to and not including the middle index. Am I just crazy or is this not making sense? Isn't this code contradicting the graph in terms of the first split?

CodePudding user response：

For the example in the image,

items = [98, 13, 274, 7, 12, 981, 5]

len(items) will be 7, and middle_index will be 7 // 2 = 3, so

left_split = items[:3] = [98, 13, 274]
right_split = items[3:] = [7, 12, 981, 5]

so you're right, the code will include the middle element in the right split, wheras it is included in the left split in the image.

However, this doesn't mean that the code doesn't make sense, since the merge function is symmetric with respect to left and right, it doesn't make any assumptions that one of the lists is larger than the other; as soon as either list has become empty during the merge, the remaining other list will be appended to the end of the result.

In fact, the exact split point is irrelevant for the sorting result, the algorithm is just more efficient if it is as close as possible to the middle, since this minimizes the larger of the two lengths of each split.