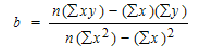How R calculates the Regression coefficients using lm() function-CodePudding

I wanted to replicate R's calculation on estimation of regression equation on below data:

set.seed(1)
Vec = rnorm(1000, 100, 3)
DF = data.frame(X1 = Vec[-1], X2 = Vec[-length(Vec)])

Below R reports estimates of coefficients

coef(lm(X1~X2, DF))  ### slope =  -0.03871511

Then I manually estimate the regression estimate for slope

(sum(DF[,1]*DF[,2])*nrow(DF) - sum(DF[,1])*sum(DF[,2])) / (nrow(DF) * sum(DF[,1]^2) - (sum(DF[,1])^2)) ### -0.03871178

They are close but still are nor matching exactly.

Can you please help me to understand what am I missing here?

Any pointer will be very helpful.

CodePudding user response：

The problem is that X1 and X2 are switched in lm relative to the long formula.

Background

The formula for slope in lm(y ~ x) is the following where x and y each have length n and x is short for x[i] and y is short for y[i] and the summations are over i = 1, 2, ..., n.

Source of the problem

Thus the long formula in the question, also shown in (1) below, corresponds to lm(X2 ~ X1, DF) and not to lm(X1 ~ X2, DF). Either change the formula in the lm model as in (1) below or else change the long formula in the answer by replacing each occurrence of DF[, 1] in the denominator with DF[, 2] as in (2) below.

# (1)

coef(lm(X2 ~ X1, DF))[[2]]
## [1] -0.03871178

(sum(DF[,1]*DF[,2])*nrow(DF) - sum(DF[,1])*sum(DF[,2])) / 
  (nrow(DF) * sum(DF[,1]^2) - (sum(DF[,1])^2))  # as in question
## [1] -0.03871178

# (2)

coef(lm(X1 ~ X2, DF))[[2]]  # as in question
## [1] -0.03871511

(sum(DF[,1]*DF[,2])*nrow(DF) - sum(DF[,1])*sum(DF[,2])) / 
  (nrow(DF) * sum(DF[,2]^2) - (sum(DF[,2])^2))
## [1] -0.03871511

CodePudding user response：

This is not a StackOverflow question per se, but rather a stats question for the sister site.

The narrow answer is that you can look into the R sources; it generally farms off to LAPACK and BLAS but a key part of the regression calculation is specialised in order to deal (in a statistically, rather than numerical way) with low-rank cases.

Anyway, here, I believe you are 'merely' not adjusting for degrees of freedom correctly which 'almost but not quite' washes out when you use 1000 observations. A simpler case follows, along with a 'simpler' way to calculate the coefficient 'by hand' which also has the advantage of matching:

> set.seed(1)
> Vec <- rnorm(5,100,3)
> DF <- data.frame(X1=Vec[-1], X2=Vec[-length(Vec)])
> coef(lm(X1 ~ X2, DF))[2]
       X2 
-0.322898 
> cov(DF$X1, DF$X2) / var(DF$X2)
[1] -0.322898
>

CodePudding user response：

coef(lm(X1~X2, DF)) 
#     (Intercept)           X2 
#    103.83714016  -0.03871511

You can apply the formula of coefficients in OLS matrix form as below.

X = cbind(1,DF[,2])
solve(t(X) %*% (X)) %*% t(X)%*% as.matrix(DF[,1])

giving,

#            [,1]
#[1,] 103.83714016
#[2,]  -0.03871511

which is same with lm() output.

Data:

set.seed(1)
Vec = rnorm(1000, 100, 3)
DF = data.frame(X1 = Vec[-1], X2 = Vec[-length(Vec)])