I am trying to solve this system of ODEs through deSolve, dX/dt = -X*a (Y-X)b c and dY/dt = -Ya (X-Y)*b for time [0,200], a=0.30, b=0.2 but c is 1 for time [50,70] and 0 otherwise. The code I have been using is,

time <- seq(0, 200, by=1)
parameters <- c(a=0.33, b=0.2, c=1)
state <- c(X = 0, Y = 0)

    two_comp <- function(time, state, parameters){
      with(as.list(c(state, parameters)), {
        dX = -X*a   (Y-X)*b   c
        dY = -Y*a   (X-Y)*b
        return(list(c(dX, dY)))
      })
    }

out <- ode(y = state, times = time, func = two_comp, parms = parameters)
out.df = as.data.frame(out)

I have left out the time varying part of the c parameter since I can't figure out a way to include it and run it smoothly. I tried including it in the function definitions, but to no avail. Please help.

CodePudding user response：

The standard way is to use approxfun, i.e. create a time dependent signal, that we also call forcing variable:

library("deSolve")
time <- seq(0, 200, by=1)
parameters <- c(a=0.33, b=0.2, c=1)
state <- c(X = 0, Y = 0)

two_comp <- function(time, state, parameters, signal){
  cc <- signal(time)
  with(as.list(c(state, parameters)), {
    dX <- -X * a   (Y - X) * b   cc
    dY <- -Y * a   (X - Y) * b
    return(list(c(dX, dY), c = cc))
  })
}

signal <- approxfun(x = c(0, 50, 70, 200), 
                    y = c(0, 1,  0,  0), 
                    method = "constant", rule = 2)

out <- ode(y = state, times = time, func = two_comp, 
           parms = parameters, signal = signal)
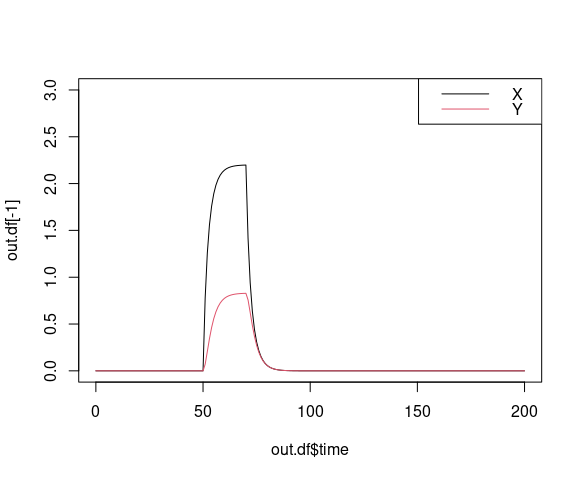
plot(out)

Note also the deSolve specific plot function and that the time dependent variable cc is used as an additional output variable.

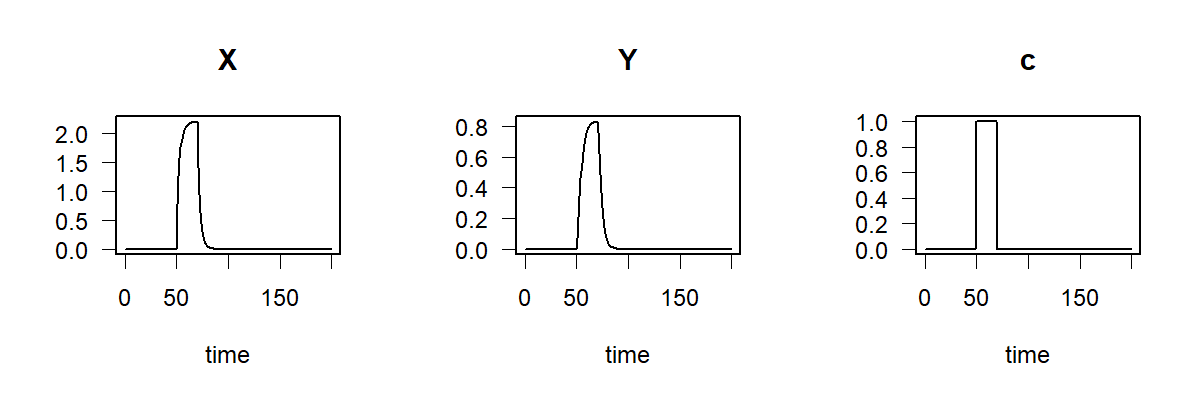
More about this can be found:

• in the ?forcings help page and
• in a