Description

Define the function unsigned mod(unsigned a, unsigned b, unsigned c); The function is to calculate and return the result of a*b%c. The range of test a, b, c is required to be greater than 0 and less than 2^31, and the program cannot use 64-bit integer (such as long long type or __int64) to solve.

Problem: a*b may overflow (beyond the representation range of the 32-bit unsigned int type). To solve this problem, the following algorithm can be used. Suppose each binary bit of the unsigned variable b is xi (i=0,1, …, 31), i=0 is the lowest bit, i=31 is the highest bit, then

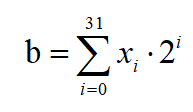
and

In the above formula, the result of a*xi is either a or 0; *2 Operation can be achieved by shifting 1 bit to the left (integer less than 2^31 *2 The result must be less than 2^32, and overflow will not occur); The result of %c is less than c, and c is less than 2^31, and the sum of it and a will not overflow. Write a complete program and implement the above algorithm by iterative method.

My Code

#pragma warning(disable:4996)
#include <stdio.h>

unsigned mod(unsigned a, unsigned b, unsigned c) {
    unsigned sum = a * ((b >> 30) & 1);
    for (int i = 29; i >= 0; i--) {
        sum = (sum << 1) % c   a * ((b >> i) & 1);
    }
    return sum % c;
}

int main() {
    //to achieve the subject requirements
    unsigned a, b, c;
    printf("Input unsigned integer numbers a, b, c:\n");
    scanf("%u %u %u", &a, &b, &c);
    printf("%u*%u%%%u=%u\n", a, b, c, mod(a, b, c));

    //to verify output results
    unsigned long long ab, bb, cb;
    ab = a;
    bb = b;
    cb = c;
    printf("%llu*%llu%%%llu=%llu", ab, bb, cb, ab * bb % cb);
}

Issues

When performing calculations with smaller numbers (such as 100*500/3), the result is correct. But when the number is close to the upper limit of the question (such as 2147483647*2147483647/3), you will get the wrong answer. I don't know why this is because I just program according to the formula given in the question, and I don't know the mathematical principle.

CodePudding user response：

The problem is here:

In mod(), you got sum = (sum << 1) % c a * ((b >> i) & 1);,
while the value of sum might be as large as a (a.k.a., a 32-bit unsigned integer).

When sum is larger than 2^31 (greater than 0b'1000 0000 0000 0000 0000 0000 0000 0000),
the left shift still will cause overflow.

CodePudding user response：

As @Uduru already pointed out, sum may become larger than 2^31 and therefore, left shifting will result in an overflow.

To prevent this, remember the following: left shifting by 1 is the same as multiplying by 2. So, (sum << 1) % c is the same as (sum * 2) % c. Now, the rules for modulo state the following:

(a * b) mod c == ((a mod c) * (b mod c)) mod c. 

So you might change the code to the following.

sum = ((sum % c) << 1) % c   a * ((b >> i) & 1);

Because c is guaranteed to be smaller than 2^31 (according to the quoted part), sum % c is also guaranteed to be smaller than 2^31.