I'm messing around with this toy problem.

Say you have a yard that's 16 x 16 feet. Each square of the grid can either be a paving square for the path or a soil square for plants. A soil square can be either reachable or unreachable.

You can start the path from any square on the outside of the grid. That's the entrance and the exit of the yard and so you start and finish there.

From any paving square, you can reach any soil square that is north, east, south or west of the paving square; you can't reach the diagonal squares.

You can only walk on the path, not on soil squares.

You want a configuration that maximises the number of reachable soil squares. Also, ideally, you want as few steps on each paving stone as possible. i.e. if you had a spiral, you'd have to walk to the end of the spiral and back again which means every paving stone except the last gets stepped on twice.

In short, you want to go from the start square to the end square in as few moves as possible and reach as many soil squares as possible.

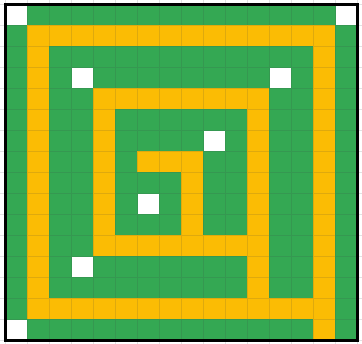
Here is a solution I came up with on paper. I haven't written any code yet to see if this is optimal. Green squares are soil, yellow squares are the path, white squares are unreachable.

There are 159 reachable green squares in this image. Out of 256 total squares, that's 62.1% green squares.

There are 89 path squares. I step on 77 of them once and 12 of them twice when I exit the yard. That's 101 total steps.

Can you find a solution with a higher proportion of green squares and a lower step count? If not, how about a higher proportion of green squares with same steps, or same green and less steps?

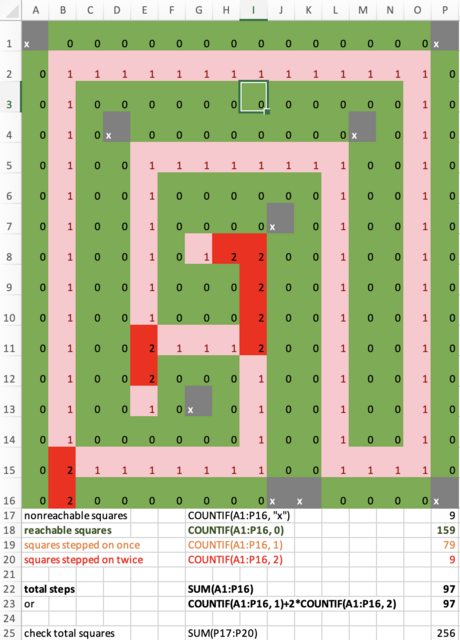
EDIT: (2021-11-7). Current best solution has been found by @sfx: 159 reachable green squares, 97 steps. Is there a better solution?

CodePudding user response：

Here is a solution with the same reachable green spaces (159), but less steps (97). I got it manually, with the help of Excel in counting and colouring.

CodePudding user response：

It's possible to get 161 reachable squares, with a small modification of your setup:

It turns out that having cycles, while good for minimizing steps, is suboptimal for maximizing reachable squares. You can gain 1 reachable square per simple cycle removed; your graph had 2.

I am fairly confident that 161 is the most possible. If examples with 162 squares exist, they must be both very rare and 'far' (in Hamming distance) from most examples with a value of 161. I used a hill-climbing method to generate all of these examples; testing small random modifications to paths and taking any with improved value.

I was able to repeatedly reach 161 squares configurations within ~10^4 iterations from an empty grid, but haven't seen any further improvements after ~10^9 iterations. The next step would be a mathematical proof of this bound.

I haven't calculated the minimal possible steps for every number of reachable squares. The example above takes 174 steps; its possible to get 173 steps (on 161 squares) with a very different arrangement:

The minimum steps for 161 reachable squares is also likely to be 173 or 172. You can do much better with 160 reachable squares, since you can keep a cycle in the graph: reconnect the cycle in the bottom left corner of my first example to remove about 50 steps (this is definitely suboptimal, too).

I can post my simulation code, if you're interested in finding further results. The main bottleneck is actually counting steps given a graph. If the graph has no cycles, its easy, since its just the sum of vertex degrees. Otherwise, this is either a travelling salesman problem or a modified Hamiltonian cycle problem.
I have a lot of optimizations around merging all degree-2 vertices, but it's basically an optimized, exponential-time depth-first search. I'd be curious if you have a faster way to compute the step counts; it seems like it should be an easy problem.