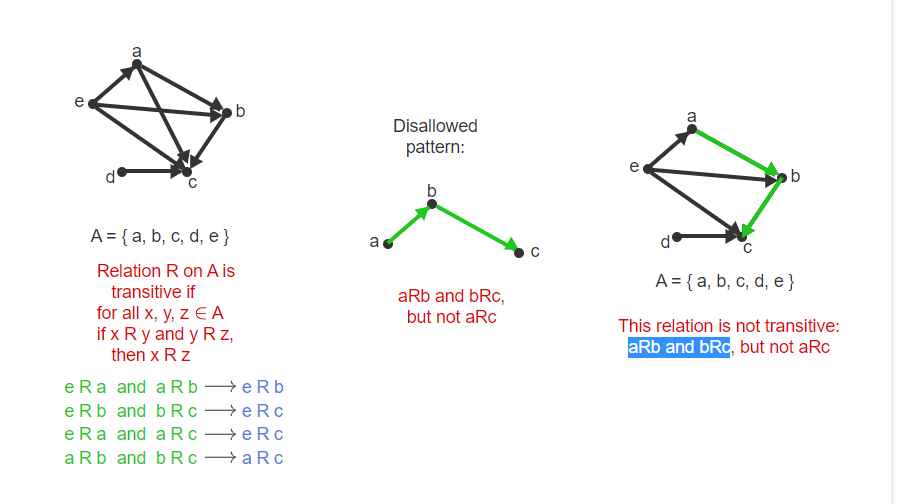
The image below shows a set that is supposed to describe a binary transitive relation:

That first arrow notation looks good at first until I saw the d node. I thought that since d cannot reach b (or any other node, yet it connects to c), it cannot be transitive?

A little bit of clarification would be great

CodePudding user response：

The first panel is fine, i.e., it is transitive. Transtivity does not require d has a (directed) path to b in this case. Transitivity, by definition, requires "if there are x and y such that d → x and x → y, then it must be d → y". Since c (which potentially play the role of x here) does not go to anywhere, as for a chain of arrows that starts from d, there is no condition that needs to be satisfied (i.e., vacuously true, when starting from d).